Bài 7.17 trang 31 sách bài tập Toán 11 - Kết nối tri thức là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ và ứng dụng của vectơ trong hình học để giải quyết các bài toán cụ thể.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 7.17 trang 31, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho hình chóp (S.ABCD) có đáy (ABCD) là hình vuông tâm (O) và các cạnh đều bằng ({rm{a}}).
Đề bài
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông tâm \(O\) và các cạnh đều bằng \({\rm{a}}\).
a) Chứng minh rằng \(SO \bot \left( {ABCD} \right)\).
b) Tính góc giữa đường thẳng \(SA\) và mặt phẳng \(\left( {SBD} \right)\).
c) Gọi \(M\) là trung điểm của cạnh \(SC\) và \(\alpha \) là góc giữa đường thẳng \(OM\) và mặt phẳng\(\left( {SBC} \right)\). Tính \({\rm{sin}}\alpha \).
Phương pháp giải - Xem chi tiết
a) Chứng minh \(SO\) vuông góc với hai đường thẳng cắt nhau nằm trên \(ABCD\) rồi suy ra \(SO \bot \left( {ABCD} \right)\).
b) Chứng minh \(AO \bot \left( {SBD} \right)\).
Tìm hình chiếu vuông góc của \(SA\) trên mặt phẳng \(\left( {SBD} \right)\), do đó góc giữa đường thẳng \(SA\) và mặt phẳng \(\left( {SBD} \right)\) bằng góc giữa hai đường thẳng \(SA\) và hình chiếu của nó.
c) Kẻ \(OK \bot BC\) tại \(K,OH \bot SK\) tại \(H\) thì ta chứng minh \(OH \bot \left( {SBC} \right)\),
Tìm hình chiếu vuông góc của \(OM\) trên mặt phẳng \(\left( {SBC} \right)\).
Góc giữa đường thẳng \(OM\) và mặt phẳng \(\left( {SBC} \right)\) bằng góc giữa hai đường thẳng \(OM\) và hình chiếu của nó.
Áp dụng tỉ số lượng giác cho tam giác vuông để tính góc.
Lời giải chi tiết
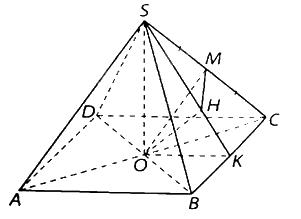
a) Có SA = SB = SC = SD = AB = BC = CD = DA = a.
Vì O là trung điểm của AC và BD nên SO vừa là đường trung tuyến, vừa là đường cao của hai tam giác cân SAC và SBD.
Ta có: \(SO \bot AC\); \(SO \bot BD\) nên \(SO \bot \left( {ABCD} \right)\).
b) Vì \(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot AO\); mà \(AO \bot BD\) (hai đường chéo hình vuông) nên \(AO \bot \left( {SBD} \right)\).
Vì \(AO \bot \left( {SBD} \right)\) nên O là hình chiếu vuông góc của A trên mặt phẳng (SBD), do đó SO là hình chiếu vuông góc của SO trên mặt phẳng (SBD).
Góc giữa đường thẳng SA và mặt phẳng (SBD) bằng góc giữa hai đường thẳng SA và SO. Mà \(\left( {SA,SO} \right) = \widehat {ASO}\) nên góc giữa đường thẳng SA và mặt phẳng (SBD) bằng góc \(\widehat {ASO}\). Xét tam giác SAC có
Có \(\left\{ \begin{array}{l}S{A^2} + S{C^2} = {a^2} + {a^2} = 2{a^2}\\A{C^2} = A{B^2} + B{C^2} = {a^2} + {a^2} = 2{a^2}\end{array} \right. \Rightarrow S{A^2} + S{C^2} = A{C^2} \Rightarrow SA \bot SC\) (định lí Pythagore đảo), suy ra tam giác SAC vuông cân tại \(S\) và \(\widehat {ASO} = {45^o}\). Vậy góc giữa đường thẳng SA và mặt phẳng (SBD) bằng \({45^o}\).
c) Kẻ \(OK \bot BC\) tại K, \(OH \bot SK\) tại H.
Có \(\left\{ \begin{array}{l}SO \bot (ABCD) \Rightarrow SO \bot BC\\OK \bot BC\end{array} \right. \Rightarrow BC \bot (SOK) \Rightarrow BC \bot OH\).
Mà \(\left\{ \begin{array}{l}BC \bot OH\\SK \bot OH\end{array} \right. \Rightarrow OH \bot (SBC)\), hay H là hình chiếu của O trên mặt phẳng (SBC).
Suy ra HM là hình chiếu vuông góc của OM trên mặt phẳng (SBC), do đó góc giữa đường thẳng OM và mặt phẳng (SBC) bằng góc giữa hai đường thẳng OM và MH, mà \(\left( {OM,MH} \right) = \widehat {OMH}\) nên góc giữa đường thẳng OM và mặt phẳng (SBC) bằng góc \(\widehat {{\rm{OMH}}}\).
Vì tam giác SAC vuông cân tại S có đường cao SO nên OA = OC = SO.
Do đó, tam giác SOC vuông cân tại O, ta lại có OM = SM = MC = \(\frac{{SC}}{2} = \frac{a}{2}\).
\(OK = \frac{a}{2}\); \(SO = \frac{{AC}}{2} = \frac{{a\sqrt 2 }}{2}\); \(SK = \sqrt {S{B^2} - B{K^2}} = \sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 3 }}{2}\).
Tam giác SOK vuông tại O, đường cao \({\rm{OH}}\) nên \({\rm{OH}}{\rm{.SK = SO}}{\rm{.OK}} \Leftrightarrow {\rm{OH}} = \frac{{{\rm{SO}} \cdot {\rm{OK}}}}{{SK}} = \frac{{a\sqrt 6 }}{6}\).
Vì tam giác OMH vuông tại H nên \({\rm{sin}}\alpha {\rm{\;}} = {\rm{sin}}\widehat {OMH} = \frac{{OH}}{{OM}} = \frac{{\sqrt 6 }}{3}\).
Bài 7.17 sách bài tập Toán 11 - Kết nối tri thức yêu cầu chúng ta giải quyết một bài toán liên quan đến vectơ trong không gian. Để giải bài toán này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về vectơ, bao gồm:
Trước khi đi vào giải chi tiết, chúng ta cần phân tích đề bài để xác định rõ yêu cầu và các dữ kiện đã cho. Thông thường, bài toán sẽ cung cấp thông tin về các điểm trong không gian và yêu cầu tính toán các đại lượng liên quan đến vectơ, chẳng hạn như:
Dưới đây là lời giải chi tiết bài 7.17 trang 31 sách bài tập Toán 11 - Kết nối tri thức. (Nội dung lời giải chi tiết sẽ được trình bày tại đây, bao gồm các bước giải, công thức sử dụng và giải thích rõ ràng từng bước. Ví dụ:)
Ví dụ: Giả sử đề bài yêu cầu tính độ dài của vectơ AB, với A(x1, y1, z1) và B(x2, y2, z2). Ta có công thức:
|AB| = √((x2 - x1)² + (y2 - y1)² + (z2 - z1)²)
Thay các tọa độ của A và B vào công thức, ta sẽ tính được độ dài của vectơ AB.
Ngoài bài 7.17, còn rất nhiều bài tập tương tự trong sách bài tập Toán 11 - Kết nối tri thức. Để giải quyết các bài tập này, bạn có thể áp dụng các phương pháp sau:
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập về vectơ, bạn có thể thử giải các bài tập sau:
Bài 7.17 trang 31 sách bài tập Toán 11 - Kết nối tri thức là một bài tập quan trọng giúp học sinh hiểu sâu hơn về vectơ và ứng dụng của vectơ trong hình học. Hy vọng với lời giải chi tiết và các phương pháp giải được trình bày ở trên, các em học sinh sẽ tự tin hơn khi giải quyết các bài tập tương tự.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Chúc các em học tập tốt!