Chào mừng các em học sinh đến với bài giải bài 7.9 trang 28 sách bài tập Toán 11 - Kết nối tri thức tại giaitoan.edu.vn. Bài viết này sẽ cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và kỹ năng giải toán.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, hỗ trợ các em trong quá trình chinh phục môn Toán.
Cho hình lăng trụ tam giác \(ABC \cdot A'B'C'\) có \(AA'\) vuông góc với mặt phẳng \(\left( {ABC} \right)\)
Đề bài
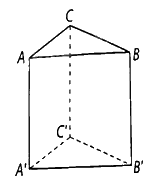
Cho hình lăng trụ tam giác \(ABC \cdot A'B'C'\) có \(AA'\) vuông góc với mặt phẳng \(\left( {ABC} \right)\) và đáy là tam giác \(ABC\) vuông tại \(B\). Chứng minh rằng:
a) \(B'B \bot \left( {A'B'C'} \right)\);
b) \(B'C \bot \left( {ABB'A'} \right)\)
Phương pháp giải - Xem chi tiết
a) Áp dụng tính chất hai mặt đáy của hình lăng trụ song song với nhau
Chỉ ra \(AA' \bot \left( {ABC} \right),AA'//BB',\left( {ABC} \right)//\left( {A'B'C'} \right)\);
b) Chỉ ra \(BC \bot AB,BC \bot BB'\) và \(BC//B'C' \Rightarrow B'C' \bot \left( {ABB'A'} \right)\)
Lời giải chi tiết
a) Vì \(AA' \bot \left( {ABC} \right),AA'//BB',\left( {ABC} \right)//\left( {A'B'C'} \right) \Rightarrow BB' \bot \left( {A'B'C'} \right)\);
b) Vì \(BC \bot AB,BC \bot BB' \Rightarrow BC \bot \left( {ABB'A'} \right)\) mà \(BC//B'C' \Rightarrow B'C' \bot \left( {ABB'A'} \right)\)
Bài 7.9 trang 28 sách bài tập Toán 11 - Kết nối tri thức thuộc chương trình học về hàm số lượng giác. Bài tập này yêu cầu học sinh vận dụng kiến thức về các phép biến đổi lượng giác cơ bản, các công thức lượng giác và các tính chất của hàm số lượng giác để giải quyết các bài toán cụ thể. Việc nắm vững kiến thức nền tảng và luyện tập thường xuyên là chìa khóa để giải quyết thành công bài tập này.
Bài tập 7.9 thường bao gồm các dạng bài sau:
Để giúp các em hiểu rõ hơn về cách giải bài tập 7.9, chúng ta sẽ đi vào giải chi tiết từng phần của bài tập. (Ở đây sẽ là lời giải chi tiết cho từng câu hỏi của bài 7.9, bao gồm các bước giải, giải thích và kết luận.)
Ví dụ 1: Rút gọn biểu thức: sin2x + cos2x
Lời giải:
Áp dụng công thức lượng giác cơ bản: sin2x + cos2x = 1
Vậy biểu thức được rút gọn là 1.
Ngoài việc giải bài tập 7.9, các em có thể tìm hiểu thêm về các chủ đề liên quan như:
Các em có thể tham khảo thêm các tài liệu sau để học tập và ôn luyện:
Hy vọng bài giải bài 7.9 trang 28 sách bài tập Toán 11 - Kết nối tri thức này sẽ giúp các em hiểu rõ hơn về kiến thức và kỹ năng giải toán lượng giác. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!