Bài 7.20 trang 34 sách bài tập Toán 11 - Kết nối tri thức với cuộc sống là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ và ứng dụng của vectơ trong hình học để giải quyết các bài toán cụ thể.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải bài tập một cách hiệu quả.
. Cho tứ diện (ABCD) có (AC = BC,AD = BD). Gọi (M) là trung điểm của (AB).
Đề bài
Cho tứ diện \(ABCD\) có \(AC = BC,AD = BD\). Gọi \(M\) là trung điểm của \(AB\). Chứng minh rằng \(\left( {CDM} \right) \bot \left( {ABC} \right)\) và \(\left( {CDM} \right) \bot \left( {ABD} \right)\).
Phương pháp giải - Xem chi tiết
Để chứng minh hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) vuông góc với nhau ta có thể dùng một trong các cách sau:
Chứng minh trong mặt phẳng này có một đường thẳng vuông góc với mặt phẳng kia. \(\left\{ \begin{array}{l}a \subset \left( \alpha \right)\\a \bot \left( \beta \right)\end{array} \right. \Rightarrow \left( \alpha \right) \bot \left( \beta \right)\).
+ Áp dụng tính chất trung tuyến của tam giác cân
Lời giải chi tiết
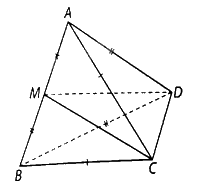
Vì \(M\) là trung điểm của \(AB\) nên \(AB \bot CM\), \(AB \bot DM\), suy ra \(AB \bot \left( {CDM} \right)\).
Vì hai mặt phẳng \(\left( {ABC} \right)\) và \(\left( {ABD} \right)\) đều chứa đường thẳng \(AB\) nên \(\left( {ABC} \right) \bot \left( {CDM} \right),\left( {ABD} \right) \bot \left( {CDM} \right)\).
Bài 7.20 thuộc chương trình sách bài tập Toán 11 - Kết nối tri thức với cuộc sống, tập trung vào việc củng cố kiến thức về vectơ và ứng dụng của chúng trong giải quyết các bài toán hình học. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản như:
Trước khi đi vào giải chi tiết, chúng ta cần phân tích đề bài để xác định rõ yêu cầu và các dữ kiện đã cho. Thông thường, bài toán 7.20 sẽ yêu cầu học sinh:
Dưới đây là lời giải chi tiết cho bài 7.20 trang 34 sách bài tập Toán 11 - Kết nối tri thức với cuộc sống. (Lưu ý: Nội dung lời giải cụ thể sẽ phụ thuộc vào đề bài chính thức của bài 7.20. Phần này sẽ được điền đầy đủ khi có đề bài cụ thể.)
Bước 1: Vẽ hình minh họa và xác định các vectơ liên quan.
Bước 2: Sử dụng các phép toán vectơ để biểu diễn các mối quan hệ giữa các vectơ.
Bước 3: Áp dụng các công thức và định lý liên quan để giải quyết bài toán.
Giả sử bài toán yêu cầu chứng minh rằng tứ giác ABCD là hình bình hành. Ta có thể sử dụng vectơ để chứng minh điều này bằng cách chứng minh rằng AB = DC và AD = BC.
Sau khi nắm vững cách giải bài 7.20, học sinh có thể tự giải các bài tập tương tự để củng cố kiến thức và kỹ năng. Một số bài tập gợi ý:
Để giải bài tập về vectơ một cách hiệu quả, học sinh cần lưu ý những điều sau:
Bài 7.20 trang 34 sách bài tập Toán 11 - Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh củng cố kiến thức về vectơ và ứng dụng của chúng trong hình học. Hy vọng với hướng dẫn chi tiết và các ví dụ minh họa trên, học sinh có thể tự tin giải quyết bài toán này và các bài tập tương tự một cách hiệu quả.
Tại giaitoan.edu.vn, chúng tôi luôn cập nhật và cung cấp các lời giải bài tập Toán 11 - Kết nối tri thức với cuộc sống đầy đủ, chính xác và dễ hiểu. Hãy truy cập website của chúng tôi để học toán online hiệu quả và đạt kết quả cao trong học tập!