Bài 7.23 trang 34 sách bài tập Toán 11 thuộc chương trình Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 7.23, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho hình lập phương (ABCD.A'B'C'D') có cạnh bằng (a).
Đề bài
Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(a\).
a) Tính côsin của góc giữa hai mặt phẳng \(\left( {A'BD} \right)\) và \(\left( {ABCD} \right)\).
b) Tính côsin của số đo góc nhị diện \(\left[ {A',BD,C'} \right]\).
Phương pháp giải - Xem chi tiết
Để tính góc giữa hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) ta có thể thực hiện cách sau:
Tìm hai đường thẳng \(a,b\) lần lượt vuông góc với hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\).
Khi đó góc giữa hai đường thẳng \(a,b\) chính là góc giữa hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\).
\(\left\{ \begin{array}{l}a \bot \left( \alpha \right)\\b \bot \left( \beta \right)\end{array} \right. \Rightarrow \widehat {\left( {\left( \alpha \right),\left( \beta \right)} \right)} = \widehat {\left( {a,b} \right)}\).
Áp dụng tính chất: Hình vuông có hai đường chéo vuông góc
Dựa vào tỉ số lượng giác trong tam giác vuông để tìm góc
Áp dụng định lí côsin trong tam giác
Lời giải chi tiết
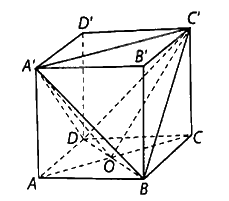
a) Gọi \(O\) là giao điểm của \(AC\) và \(BD\), ta có: \(AO \bot BD,A'O \bot BD\) nên góc giữa hai mặt phẳng \(\left( {A'BD} \right)\) và \(\left( {ABCD} \right)\) bằng góc giữa hai đường thẳng \(AO,A'O\) mà \(\left( {AO,A'O} \right) = \widehat {AOA'}\) nên góc giữa hai mặt phẳng \(\left( {A'BD} \right)\) và \(\left( {ABCD} \right)\) bằng \(\widehat {AOA'}\).
Ta có: \(OA = \frac{{a\sqrt 2 }}{2},OA' = \sqrt {O{A^2} + A{A^{{\rm{'}}2}}} = \frac{{a\sqrt 6 }}{2}\).
Suy ra \({\rm{cos}}\widehat {AOA'} = \frac{{AO}}{{A'O}} = \frac{{\sqrt 3 }}{3}\).
b) Vì \(A'O \bot BD,CO' \bot BD\) nên góc nhị diện \(\left[ {A',BD} \right.\),\(\left. {C'} \right]\) bằng \(\widehat {{A^{\rm{'}}}OC'}\).
Ta có \(OA' = OC' = \frac{{a\sqrt 6 }}{2},A'C' = a\sqrt 2 \) nên \({\rm{cos}}\widehat {A'OC'} = \frac{{O{A^{{\rm{'}}2}} + O{C^2} - A'{C^2}}}{{2 \cdot OA' \cdot OC'}} = \frac{1}{3}\).
Bài 7.23 trang 34 sách bài tập Toán 11 Kết nối tri thức yêu cầu học sinh vận dụng kiến thức về đạo hàm để tìm cực trị của hàm số. Để giải bài tập này một cách hiệu quả, chúng ta cần thực hiện các bước sau:
Đề bài: (Sách bài tập Toán 11 Kết nối tri thức)
Tìm các điểm cực trị của các hàm số sau:
a) f(x) = x3 - 3x2 + 2
b) f(x) = -x4 + 4x2
a) f(x) = x3 - 3x2 + 2
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| f'(x) | + | - | + | |
| f(x) | Đồng biến | Nghịch biến | Đồng biến |
Kết luận: Hàm số đạt cực đại tại x = 0, f(0) = 2 và đạt cực tiểu tại x = 2, f(2) = -2
b) f(x) = -x4 + 4x2
| x | -∞ | -√2 | 0 | √2 | +∞ |
|---|---|---|---|---|---|
| f'(x) | + | - | + | - | |
| f(x) | Đồng biến | Nghịch biến | Đồng biến | Nghịch biến |
Kết luận: Hàm số đạt cực đại tại x = -√2, f(-√2) = 2 và x = √2, f(√2) = 2; đạt cực tiểu tại x = 0, f(0) = 0
Hy vọng với lời giải chi tiết và hướng dẫn trên, các em học sinh sẽ hiểu rõ hơn về cách giải bài 7.23 trang 34 sách bài tập Toán 11 Kết nối tri thức và tự tin hơn trong việc giải các bài tập tương tự.