Bài 4.4 trang 55 sách bài tập Toán 11 - Kết nối tri thức là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ và ứng dụng của vectơ trong hình học để giải quyết các bài toán cụ thể.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4.4 trang 55, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD.
Đề bài
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD. Gọi P là một điểm thuộc cạnh BC sao cho PC = 2PB.
a) Xác định giao điểm của đường thẳng BD và mặt phẳng (MNP).
b) Xác định giao điểm của đường thẳng AC và mặt phẳng (MNP).
c) Xác định giao điểm của đường thẳng AD và mặt phẳng (MNP).
Phương pháp giải - Xem chi tiết
Để xác định giao điểm của đường thẳng d và mặt phẳng (P), ta tìm một đường thẳng trong mặt phẳng (P) sao cho đường thẳng đó đồng phẳng với d. Xác giao điểm của đường thẳng đó với d. Giao điểm ấy chính là giao điểm giữa đường thẳng d và mặt phẳng (P).
Lời giải chi tiết
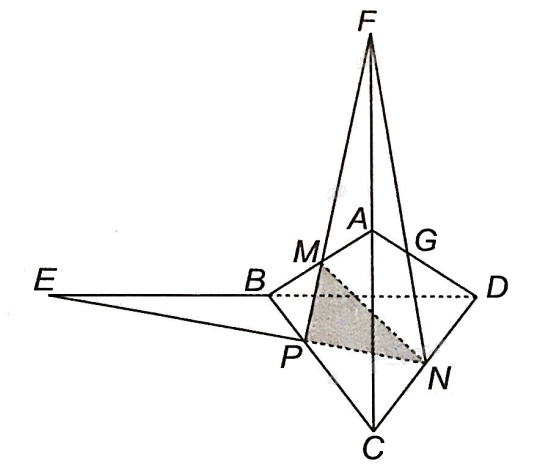
a) Trong mặt phẳng (BCD): Gọi E là giao điểm của BD và PN.
Vậy giao điểm của đường thẳng BD và mặt phẳng (MNP) là điểm E.
b) Trong mặt phẳng (ABC): gọi F là giao điểm của AC và MP.
Vậy giao điểm của đường thẳng AC và mặt phẳng (MNP) là điểm F.
c) Trong mặt phẳng (ADC): gọi G là giao điểm của AD và NF.
Vậy giao điểm của đường thẳng AD và mặt phẳng (MNP) là điểm G.
Bài 4.4 trang 55 sách bài tập Toán 11 - Kết nối tri thức thường xoay quanh các chủ đề về vectơ, bao gồm:
Để giải quyết bài 4.4 trang 55 một cách hiệu quả, bạn cần nắm vững các kiến thức cơ bản này. Dưới đây là hướng dẫn chi tiết từng bước để giải bài tập:
Đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Xác định các vectơ đã cho, các điểm và các yếu tố liên quan. Vẽ hình minh họa để dễ dàng hình dung bài toán.
Sử dụng các kiến thức và công thức về vectơ để giải quyết bài toán. Ví dụ:
Lưu ý lựa chọn hệ tọa độ phù hợp để đơn giản hóa bài toán.
Thực hiện các phép tính toán một cách cẩn thận và chính xác. Kiểm tra lại kết quả để đảm bảo tính đúng đắn. So sánh kết quả với các đáp án đã cho (nếu có).
Ví dụ minh họa (giả định):
Cho tam giác ABC với A(1;2), B(3;4), C(5;6). Tìm tọa độ điểm D sao cho AD = BC.
Các dạng bài tập thường gặp:
Lời khuyên khi học tập:
Giaitoan.edu.vn hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải quyết bài 4.4 trang 55 sách bài tập Toán 11 - Kết nối tri thức và đạt kết quả tốt trong môn học Toán.
| Công thức | Mô tả |
|---|---|
| a + b | Phép cộng vectơ |
| k.a | Phép nhân vectơ với một số thực |
| a.b | Tích vô hướng của hai vectơ |