Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài tập 4.2 trang 55 sách bài tập Toán 11 - Kết nối tri thức với cuộc sống. Bài viết này sẽ giúp bạn nắm vững kiến thức và kỹ năng giải toán, tự tin hơn trong quá trình học tập.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải bài 4.2 trang 55 một cách cẩn thận, chi tiết, kèm theo các bước giải rõ ràng.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của các cạnh BC, CD.
Đề bài
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của các cạnh BC, CD.
a) Xác định giao tuyến của hai mặt phẳng (SAM) và (SCD).
b) Xác định giao tuyến của hai mặt phẳng (SBN) và (SAD).
c) Xác định giao tuyến của hai mặt phẳng (SAM) và (SBN).
Phương pháp giải - Xem chi tiết
Để xác định giao tuyến của hai mặt phẳng, ta tìm hai điểm chung (phân biệt) của hai mặt phẳng đó.
Lời giải chi tiết
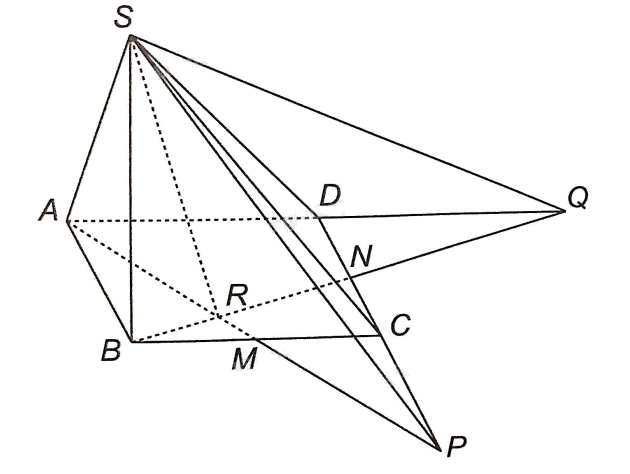
a) Ta thấy S là điểm chung thứ nhất của hai mặt phẳng (SAM) và (SCD).
Trong mặt phẳng (ABCD): Gọi P là giao điểm của AM và CD => P là điểm chung thứ hai của mặt phẳng (SAM) và (SCD).
Vậy SP là giao tuyến của (SAM) và (SCD).
b) Ta thấy S là điểm chung thứ nhất của hai mặt phẳng (SBN) và (SAD).
Trong mặt phẳng (ABCD): Gọi Q là giao điểm của AM và CD => P là điểm chung thứ hai của mặt phẳng (SBN) và (SAD).
Vậy SQ là giao tuyến của (SBN) và (SAD).
c) Ta thấy S là điểm chung thứ nhất của hai mặt phẳng (SAM) và (SBN).
Trong mặt phẳng (ABCD): Gọi R là giao điểm của AM và BN => R là điểm chung thứ hai của mặt phẳng (SAM) và (SBN).
Vậy SR là giao tuyến của (SAM) và (SBN).
Bài 4.2 trang 55 sách bài tập Toán 11 - Kết nối tri thức với cuộc sống thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức về vectơ trong không gian để giải quyết các bài toán hình học. Để giải quyết bài toán này một cách hiệu quả, chúng ta cần nắm vững các khái niệm cơ bản như:
Nội dung bài toán 4.2 trang 55: Bài toán yêu cầu chúng ta sử dụng kiến thức về tích vô hướng để chứng minh một đẳng thức vectơ hoặc giải quyết một bài toán liên quan đến góc giữa hai vectơ trong không gian.
Để giải bài 4.2 trang 55, chúng ta sẽ tiến hành theo các bước sau:
Giả sử bài toán 4.2 yêu cầu chứng minh đẳng thức vectơ a.b = |a||b|cos(θ), trong đó θ là góc giữa hai vectơ a và b. Chúng ta có thể giải bài toán này như sau:
Bước 1: Chọn hệ tọa độ Oxyzu.
Bước 2: Giả sử vectơ a có tọa độ (x1, y1, z1) và vectơ b có tọa độ (x2, y2, z2).
Bước 3: Tính tích vô hướng a.b = x1x2 + y1y2 + z1z2.
Bước 4: Tính độ dài của vectơ a: |a| = √(x12 + y12 + z12) và độ dài của vectơ b: |b| = √(x22 + y22 + z22).
Bước 5: Tính cos(θ) = (x1x2 + y1y2 + z1z2) / (|a||b|).
Bước 6: Thay thế các giá trị đã tính vào đẳng thức a.b = |a||b|cos(θ) để chứng minh đẳng thức.
Giaitoan.edu.vn hy vọng rằng với hướng dẫn chi tiết này, bạn sẽ tự tin giải quyết bài 4.2 trang 55 sách bài tập Toán 11 - Kết nối tri thức với cuộc sống một cách hiệu quả. Chúc bạn học tập tốt!