Bài 7.46 trang 42 sách bài tập Toán 11 thuộc chương trình học Toán 11 Kết nối tri thức với cuộc sống. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho hình chóp \(S.ABCD\)có tất cả các cạnh đều bằng a
Đề bài
Cho hình chóp \(S.ABCD\)có tất cả các cạnh đều bằng a, gọi \(O\) là giao điểm của \(AC\)và\(BD\). Khoản cách từ điểm \(O\) đến mặt phẳng \(\left( {SBC} \right)\) bằng
A. \(\frac{{a\sqrt 6 }}{6}\).
B. \(\frac{{a\sqrt 3 }}{3}\).
C. \(\frac{{a\sqrt 3 }}{2}\).
D. \(\frac{{a\sqrt 6 }}{3}\).
Phương pháp giải - Xem chi tiết
Tìm hình chiếu vuông góc của \(O\) lên \(\left( {SBC} \right)\) là điểm \(H\).Tính \(OH\) theo công thức đường cao của tam giác vuông.
Lời giải chi tiết
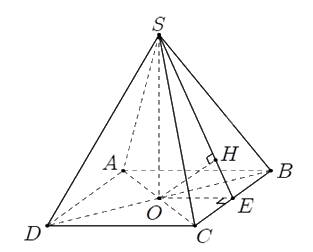
Tính khoảng cách từ \(O\) tới \(mp\left( {SBC} \right)\):
Gọi \(E\) là trung điểm của \(BC\).
Theo giả thiết \(SO \bot \left( {ABCD} \right) \supset BC\).
\( \Rightarrow \) \(\left\{ \begin{array}{l}BC \bot SO \subset \left( {SOE} \right)\\BC \bot OE \subset \left( {SOE} \right)\\OE \cap SO = O\end{array} \right.\) \( \Rightarrow \) \(BC \bot \left( {SOE} \right)\) mà \(BC \subset \left( {SBC} \right)\)\( \Rightarrow \) \(\left( {SBC} \right) \bot \left( {SOE} \right)\).
Gọi \(H\) là hình chiếu vuông góc của \(O\) lên \(SE\)\( \Rightarrow OH \bot SE = \left( {SBC} \right) \cap \left( {SOE} \right)\), suy ra \(OH \bot \left( {SBC} \right)\) nên \(d\left( {O,\left( {SBC} \right)} \right) = OH\).
Ta có \(SO = \sqrt {S{C^2} - O{C^2}} = \sqrt {{a^2} - {{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2}} = \frac{{a\sqrt 2 }}{2}\).
Trong \(\Delta SOE\) vuông tại \(O\), ta có:
\(\frac{1}{{O{H^2}}} = \frac{1}{{O{E^2}}} + \frac{1}{{O{S^2}}} = \frac{1}{{{{\left( {\frac{a}{2}} \right)}^2}}} + \frac{1}{{{{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2}}} = \frac{6}{{{a^2}}}\) \( \Rightarrow \) \(OH = \frac{a}{{\sqrt 6 }}\)
\( \Rightarrow \)\(d\left( {O,\left( {SCD} \right)} \right) = OH = \frac{a}{{\sqrt 6 }} = \frac{{a\sqrt 6 }}{6}\).
Bài 7.46 trang 42 sách bài tập Toán 11 - Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh tìm đạo hàm của hàm số, xét dấu đạo hàm để xác định khoảng đồng biến, nghịch biến của hàm số, và tìm cực trị của hàm số.
Trước khi bắt đầu giải bài tập, học sinh cần đọc kỹ đề bài để hiểu rõ yêu cầu của bài toán. Xác định hàm số cần xét, các điều kiện ràng buộc (nếu có), và mục tiêu của bài toán (ví dụ: tìm đạo hàm, tìm cực trị, khảo sát hàm số).
Để giải bài 7.46, học sinh cần nắm vững các kiến thức cơ bản về đạo hàm, bao gồm:
(Ở đây sẽ là lời giải chi tiết của bài 7.46, bao gồm các bước giải, giải thích rõ ràng, và kết quả cuối cùng. Lời giải sẽ được trình bày một cách logic và dễ hiểu, sử dụng các ký hiệu toán học chính xác.)
Để giúp học sinh hiểu rõ hơn về cách giải bài 7.46, chúng ta sẽ xem xét một số ví dụ minh họa và bài tập tương tự:
Khi giải bài tập về đạo hàm, học sinh cần lưu ý một số điểm sau:
Đạo hàm có rất nhiều ứng dụng trong thực tế, bao gồm:
Bài 7.46 trang 42 sách bài tập Toán 11 - Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm. Hy vọng rằng với hướng dẫn chi tiết và các ví dụ minh họa trên, các em học sinh sẽ tự tin giải quyết bài tập này và các bài tập tương tự.