Bài 1.29 trang 24 sách bài tập Toán 11 - Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về dãy số, cấp số cộng và cấp số nhân. Bài tập này thường yêu cầu học sinh vận dụng các công thức và tính chất của dãy số để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 1.29 trang 24, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
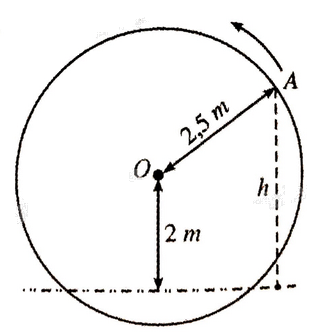
Một chiếc guồng nước có dạng hình tròn bán kính 2,5m; trục của nó đặt cách mặt nước 2m (hình bên).
Đề bài
Một chiếc guồng nước có dạng hình tròn bán kính 2,5m; trục của nó đặt cách mặt nước 2m (hình bên). Khi guồng quay đều, khoảng cách h (mét) tính từ một chiếc gầu gắn tại điểm A trên guồng đến mặt nước là \(h = \left| y \right|\) trong đó \(y = 2 + 2,5\sin 2\pi \left( {x - \frac{1}{4}} \right)\) với x là thời gian quay của guồng \(\left( {x \ge 0} \right),\) tính bằng phút; ta quy ước rằng \(y > 0\) khi gầu ở trên mặt nước và \(y < 0\) khi gầu ở dưới mặt nước.
a) Khi nào chiếc gầu ở vị trí cao nhất? Thấp nhất?
b) Chiếc gầu cách mặt nước 2 mét lần đầu tiên khi nào?
Phương pháp giải - Xem chi tiết
* Sử dụng kiến thức \( - 1 \le \sin x \le 1\) với mọi x
* Sử dụng cách giải phương trình \(\sin x = m\) (1)
+ Nếu \(\left| m \right| > 1\) thì phương trình (1) vô nghiệm.
+ Nếu \(\left| m \right| \le 1\) thì tồn tại duy nhất số \(\alpha \in \left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) thỏa mãn \(\sin \alpha = m\).
Khi đó, phương trình (1) tương đương với:
\(\sin x = m \Leftrightarrow \sin x = \sin \alpha \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = \pi - \alpha + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\)
Lời giải chi tiết
a) Vì \( - 1 \le \sin 2\pi \left( {x - \frac{1}{4}} \right) \le 1\) nên \( - 2,5 \le 2,5\sin 2\pi \left( {x - \frac{1}{4}} \right) \le 2,5\)
Do đó, \( - 0,5 = 2 - 2,5 \le 2 + 2,5\sin 2\pi \left( {x - \frac{1}{4}} \right) \le 2 + 2,5 = 4,5\;\forall x \in \mathbb{R}\)
Suy ra, gầu ở vị trí cao nhất khi \(\sin 2\pi \left( {x - \frac{1}{4}} \right) = 1 \Leftrightarrow 2\pi \left( {x - \frac{1}{4}} \right) = \frac{\pi }{2} + k2\pi \Leftrightarrow x = \frac{1}{2} + k\left( {k \in \mathbb{Z}} \right)\)
Vì gầu ở vị trí cao nhất tại các thời điểm \(\frac{1}{2},\frac{3}{2},\frac{5}{2},...\) phút
Tương tự, gầu ở vị trí thấp nhất khi \(\sin 2\pi \left( {x - \frac{1}{4}} \right) = - 1 \Leftrightarrow 2\pi \left( {x - \frac{1}{4}} \right) = - \frac{\pi }{2} + k2\pi \Leftrightarrow x = k\left( {k \in \mathbb{Z}} \right)\)
Vì gầu ở vị trí cao nhất tại các thời điểm 0, 1, 2, 3… phút
b) Gầu cách mặt nước 2m khi \(2 + 2,5\sin 2\pi \left( {x - \frac{1}{4}} \right) = 2 \Leftrightarrow 2,5\sin 2\pi \left( {x - \frac{1}{4}} \right) = 0 \Leftrightarrow 2\pi \left( {x - \frac{1}{4}} \right) = k\pi \Leftrightarrow x = \frac{1}{4} + \frac{k}{2}\left( {k \in \mathbb{Z}} \right)\)
Vậy chiếc gầu cách mặt nước 2m lần đầu tại thời điểm \(x = \frac{1}{4}\) phút
Bài 1.29 trang 24 sách bài tập Toán 11 - Kết nối tri thức yêu cầu học sinh giải quyết một bài toán liên quan đến dãy số, thường là cấp số cộng hoặc cấp số nhân. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về dãy số, bao gồm:
Để cung cấp lời giải chi tiết, chúng ta cần biết nội dung cụ thể của bài 1.29. Giả sử bài toán yêu cầu tìm số hạng thứ n của một cấp số cộng, ta có thể áp dụng công thức:
un = u1 + (n - 1)d
Trong đó:
Để tìm tổng n số hạng đầu tiên của cấp số cộng, ta có thể áp dụng công thức:
Sn = (n/2)(u1 + un) hoặc Sn = (n/2)[2u1 + (n - 1)d]
Tương tự, đối với cấp số nhân, ta có:
un = u1qn-1
Sn = u1(1 - qn) / (1 - q) (với q ≠ 1)
Ví dụ minh họa:
Giả sử bài 1.29 yêu cầu tìm số hạng thứ 10 của cấp số cộng có số hạng đầu tiên là 2 và công sai là 3. Ta có:
u10 = 2 + (10 - 1) * 3 = 2 + 9 * 3 = 2 + 27 = 29
Vậy số hạng thứ 10 của cấp số cộng là 29.
Ngoài việc tìm số hạng thứ n và tổng n số hạng đầu tiên, bài 1.29 và các bài tập tương tự có thể yêu cầu học sinh:
Để nắm vững kiến thức về dãy số và cấp số, học sinh có thể tham khảo các tài liệu sau:
Bài 1.29 trang 24 sách bài tập Toán 11 - Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về dãy số. Bằng cách nắm vững các công thức và tính chất của dãy số, cùng với việc luyện tập thường xuyên, học sinh có thể tự tin giải quyết các bài toán liên quan đến dãy số một cách hiệu quả.