Bài 7.27 trang 37 sách bài tập Toán 11 thuộc chương trình Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 7.27, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(a\). Tính theo \(a\) khoảng cách
Đề bài
Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(a\). Tính theo \(a\) khoảng cách
a) Giữa hai đường thẳng \(AB\) và \(C'D'\).
b) Giữa đường thẳng \(AC\) và \(\left( {A'B'C'D'} \right)\).
c) Từ điểm \(A\) đường thẳng \(B'D'\).
d) Giữa hai đường thẳng \(AC\) và \(B'D'\).
Phương pháp giải - Xem chi tiết
a)
Bước 1: Xác định đường vuông góc chung hai đường thẳng
Bước 2: Tính độ dài đoạn vuông góc chung hai đường thẳng
b) Vì \(AC\parallel \left( {A'B'C'D'} \right)\) nên \(d\left( {AC,\left( {A'B'C'D'} \right)} \right) = d\left( {A,\left( {A'B'C'D'} \right)} \right) = AA'\).
c) Gọi \(O'\) là giao điểm của \(A'C'\) và \(B'D'\) ta có \(AO' \bot B'D'\), theo định lý Pythagore áp dụng cho tam giác \(AA'O'\) vuông tại \(A'\) thì \(AO' = \frac{{a\sqrt 6 }}{2}\).
Do đó, \(d\left( {A,B'D'} \right) = AO'\).
d) Ta có \(d\left( {AC,B'D'} \right) = d\left( {AC,\left( {A'B'C'D'} \right)} \right) = d\left( {A,\left( {A'B'C'D'} \right)} \right) = AA'\).
Lời giải chi tiết
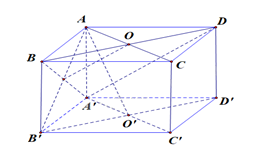
a) Vì \(BC'\) vuông góc với cả hai đường thẳng \(AB\)và \(C'D'\) nên \(d\left( {AB,C'D'} \right) = BC' = a\sqrt 2 \).
b) Vì \(AC\parallel \left( {A'B'C'D'} \right)\) nên \(d\left( {AC,\left( {A'B'C'D'} \right)} \right) = d\left( {A,\left( {A'B'C'D'} \right)} \right) = AA' = a\).
c) Gọi \(O'\) là giao điểm của \(A'C'\) và \(B'D'\) ta có \(AO' \bot B'D'\), theo định lý Pythagore áp dụng cho tam giác \(AA'O'\) vuông tại \(A'\) thì \(AO' = \frac{{a\sqrt 6 }}{2}\). Do đó, \(d\left( {A,B'D'} \right) = AO' = \frac{{a\sqrt 6 }}{2}\).
d) Ta có \(d\left( {AC,B'D'} \right) = d\left( {AC,\left( {A'B'C'D'} \right)} \right) = d\left( {A,\left( {A'B'C'D'} \right)} \right) = AA' = a\).
Bài 7.27 yêu cầu học sinh sử dụng kiến thức về đạo hàm để tìm cực trị của hàm số. Đây là một dạng bài tập điển hình trong chương trình Toán 11, đòi hỏi học sinh phải nắm vững các bước sau:
Để giải bài 7.27, chúng ta cần phân tích kỹ đề bài và áp dụng các bước đã nêu ở trên. Giả sử hàm số được cho là:
f(x) = x3 - 3x2 + 2
f'(x) = 3x2 - 6x
Giải phương trình f'(x) = 0:
3x2 - 6x = 0
3x(x - 2) = 0
Vậy, x = 0 hoặc x = 2 là các điểm tới hạn.
Xét các khoảng:
Tại x = 0, f'(x) chuyển từ dương sang âm, hàm số đạt cực đại.
Tại x = 2, f'(x) chuyển từ âm sang dương, hàm số đạt cực tiểu.
f(0) = 03 - 3(0)2 + 2 = 2 (cực đại)
f(2) = 23 - 3(2)2 + 2 = 8 - 12 + 2 = -2 (cực tiểu)
Hàm số f(x) = x3 - 3x2 + 2 đạt cực đại tại x = 0 với giá trị là 2 và đạt cực tiểu tại x = 2 với giá trị là -2.
Để nắm vững kiến thức về cực trị của hàm số, các em học sinh nên luyện tập thêm các bài tập tương tự. Một số bài tập gợi ý:
Giaitoan.edu.vn là website học Toán online uy tín, cung cấp lời giải chi tiết, dễ hiểu cho các bài tập Toán từ lớp 6 đến lớp 12. Chúng tôi luôn cập nhật kiến thức mới nhất và phương pháp giải bài tập hiệu quả, giúp các em học sinh học Toán một cách dễ dàng và thú vị.