Bài 7.53 trang 43 sách bài tập Toán 11 - Kết nối tri thức với cuộc sống là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải bài tập một cách hiệu quả.
Cho hình chóp tứ giác đều \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh bằng \(a\)
Đề bài
Cho hình chóp tứ giác đều \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh bằng \(a\), cạnh bên \(SA = \frac{{a\sqrt 5 }}{2}\). Gọi \(SM,SN\) lần lượt là đường cao của tam giác \(SAD\) và tam giác \(SBC\).
a) Chứng minh rằng \(\left( {SMN} \right) \bot \left( {ABCD} \right)\).
b) Tính số đo của góc nhị diện \([S,AD,B]\).
Xác định
c) Tính theo a thể tích khối chóp \(S.ABCD\).
Phương pháp giải - Xem chi tiết
a) Chứng minh rằng \(\left( {SMN} \right) \bot \left( {ABCD} \right)\).
Chứng minh mặt phẳng \(\left( {ABCD} \right)\) chứa \(BC \bot \) \(\left( {SMN} \right).\)
b) Tính số đo của góc nhị diện \([S,AD,B]\).
c) Tính theo a thể tích khối chóp \(S.ABCD\).
Lời giải chi tiết
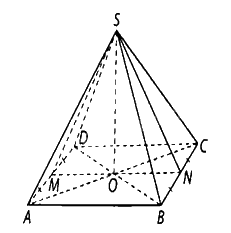
a) Gọi \(O\) là giao điểm của \(AC\) và \(BD\).
Ta có: \(AD \bot SM,AD//BC\) nên \(BC \bot SM\), mà \(BC \bot SN\), suy ra \(BC \bot \left( {SMN} \right).\)
Do đó \(\left( {SMN} \right) \bot \left( {ABCD} \right)\).
b) Vì \(MN\) đi qua \(O\) và \(OM \bot AD,SM \bot AD\) nên \(\left[ {S,AD,B} \right] = \widehat {SMO}\), ta tính được\(SM = SN = MN = a\). Do đó tam giác \(SMN\) đều, suy ra \(\widehat {SMN} = {60^ \circ }\).
Vậy \(\left[ {S,AD,B} \right] = {60^ \circ }\).
c) Ta có: \(SO = \frac{{a\sqrt 3 }}{2},{S_{ABCD}} = {a^2}\), suy ra \({V_{S.ABCD}} = \frac{1}{3} \cdot {S_{ABCD}} \cdot SO = \frac{{{a^3}\sqrt 3 }}{6}\).
Bài 7.53 trang 43 sách bài tập Toán 11 - Kết nối tri thức với cuộc sống là một bài toán ứng dụng thực tế, đòi hỏi học sinh phải hiểu rõ về đạo hàm và cách sử dụng đạo hàm để giải quyết các vấn đề liên quan đến tốc độ thay đổi của một đại lượng.
Trước khi đi vào giải bài, chúng ta cần phân tích kỹ đề bài để xác định rõ các yếu tố quan trọng: đại lượng cần tìm, các điều kiện cho trước và mối quan hệ giữa các đại lượng đó. Việc phân tích đề bài một cách cẩn thận sẽ giúp chúng ta xây dựng phương án giải quyết bài toán một cách hiệu quả.
Để giải bài 7.53, chúng ta sẽ sử dụng phương pháp đạo hàm để tìm ra mối quan hệ giữa các đại lượng và từ đó giải quyết bài toán. Cụ thể, chúng ta sẽ thực hiện các bước sau:
Dưới đây là lời giải chi tiết cho bài 7.53 trang 43 sách bài tập Toán 11 - Kết nối tri thức với cuộc sống:
(Giải bài toán cụ thể ở đây - ví dụ về một bài toán liên quan đến vận tốc, gia tốc, hoặc tối ưu hóa một hàm số. Cần có các bước giải chi tiết, kèm theo giải thích rõ ràng.)
Để giúp học sinh hiểu rõ hơn về phương pháp giải, chúng ta sẽ xem xét một ví dụ minh họa:
(Ví dụ minh họa với một bài toán tương tự, giải thích chi tiết từng bước.)
Ngoài bài 7.53, còn rất nhiều bài tập ứng dụng khác trong chương trình Toán 11. Để nâng cao kiến thức và kỹ năng, học sinh nên tự tìm hiểu và giải thêm các bài tập tương tự. Việc làm này sẽ giúp học sinh hiểu sâu hơn về đạo hàm và ứng dụng của nó trong thực tế.
Bài 7.53 trang 43 sách bài tập Toán 11 - Kết nối tri thức với cuộc sống là một bài tập quan trọng, giúp học sinh rèn luyện kỹ năng giải quyết các bài toán ứng dụng thực tế. Hy vọng với lời giải chi tiết và các ví dụ minh họa, học sinh sẽ nắm vững kiến thức và tự tin giải quyết các bài tập tương tự.
Giaitoan.edu.vn luôn đồng hành cùng học sinh trên con đường chinh phục môn Toán. Hãy truy cập website của chúng tôi để tìm hiểu thêm về các bài giải khác và các tài liệu học tập hữu ích.