Bài 8.14 trang 51 sách bài tập Toán 11 - Kết nối tri thức với cuộc sống là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về đường thẳng và mặt phẳng trong không gian để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải bài tập một cách hiệu quả.
. Hai bạn An và Bình không quen biết nhau và đều học xa nhà
Đề bài
Hai bạn An và Bình không quen biết nhau và đều học xa nhà. Xác suất để bạn An về thăm nhà vào ngày Chủ nhật là 0,2 và của bạn Bình là 0,25. Dùng sơ đồ hình cây để tính xác suất vào ngày Chủ nhật:
a) Cả hai bạn đều về thăm nhà.
b) Có ít nhất một bạn về thăm nhà.
c) Cả hai bạn đều không về thăm nhà.
d) Chỉ có bạn An về thăm nhà.
e) Có đúng một bạn về thăm nhà.
Phương pháp giải - Xem chi tiết
Gọi \(A,B\) tương ứng là các biến cố: "Bạn \(An\) về thăm nhà vào ngày Chủ nhật" và "Bạn Bình về thăm nhà vào ngày Chủ nhật". \(A\) và \(B\) là hai biến cố độc lập.
Ta có sơ đồ hình cây:
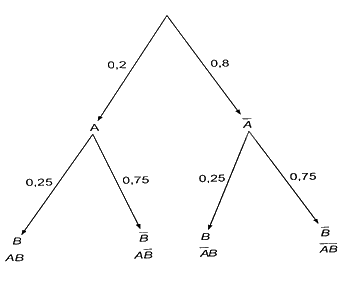
Từ đó suy ra xác suất cần tìm
Lời giải chi tiết
Gọi \(A,B\) tương ứng là các biến cố: "Bạn \(An\) về thăm nhà vào ngày Chủ nhật" và "Bạn Bình về thăm nhà vào ngày Chủ nhật". \(A\) và \(B\) là hai biến cố độc lập.
Ta có sơ đồ hình cây:
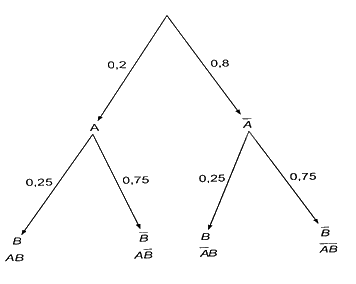
a) \(P\left( {AB} \right) = 0,2 \cdot 0,25 = 0,05\).
b) \(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {AB} \right) = 0,2 + 0,25 - 0,05 = 0,4\).
c) \(P\left( {\overline A \,\overline B } \right) = 0,8 \cdot 0,75 = 0,6\).
d) \(P\left( {A\overline B } \right) = 0,2 \cdot 0,75 = 0,15\).
e) \(P\left( {A\overline B \cup \overline A B} \right) = P\left( {A\overline B } \right) + P\left( {\overline A B} \right) = 0,2 \cdot 0,75 + 0,8 \cdot 0,25 = 0,35\).
Bài 8.14 trang 51 sách bài tập Toán 11 - Kết nối tri thức với cuộc sống là một bài toán thuộc chương trình hình học không gian, cụ thể là phần về đường thẳng và mặt phẳng. Để giải bài toán này, học sinh cần nắm vững các kiến thức cơ bản như:
Trước khi bắt tay vào giải bài toán, học sinh cần đọc kỹ đề bài, xác định rõ các yếu tố đã cho và yêu cầu của bài toán. Sau đó, cần phân tích đề bài để tìm ra hướng giải phù hợp. Thông thường, để giải bài toán về đường thẳng và mặt phẳng, chúng ta cần:
(Nội dung lời giải chi tiết bài 8.14 sẽ được trình bày tại đây, bao gồm các bước giải cụ thể, các công thức và định lý được sử dụng, và các giải thích rõ ràng để học sinh dễ hiểu. Lời giải sẽ được trình bày một cách logic và khoa học, đảm bảo tính chính xác và đầy đủ.)
Để giúp học sinh hiểu rõ hơn về cách giải bài toán này, chúng ta sẽ xem xét một số ví dụ minh họa và bài tập tương tự. Các ví dụ này sẽ giúp học sinh củng cố kiến thức và kỹ năng giải bài tập về đường thẳng và mặt phẳng.
Bài 8.14 trang 51 sách bài tập Toán 11 - Kết nối tri thức với cuộc sống là một bài toán quan trọng, giúp học sinh củng cố kiến thức về đường thẳng và mặt phẳng trong không gian. Hy vọng rằng, với hướng dẫn chi tiết và các ví dụ minh họa, học sinh có thể giải bài toán này một cách dễ dàng và hiệu quả.
| Công thức | Mô tả |
|---|---|
| Phương trình đường thẳng | ... |
| Phương trình mặt phẳng | ... |
| Góc giữa đường thẳng và mặt phẳng | ... |
(Nội dung bảng sẽ được điền đầy đủ các công thức liên quan đến bài toán.)
Giaitoan.edu.vn luôn đồng hành cùng học sinh trên con đường chinh phục môn Toán. Chúc các em học tập tốt!