Bài 4.20 trang 60 sách bài tập Toán 11 - Kết nối tri thức là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ và ứng dụng của vectơ trong hình học để giải quyết các bài toán cụ thể.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4.20 trang 60, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
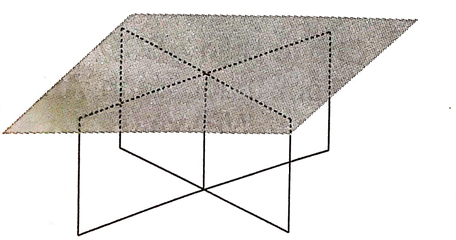
Một chiếc thang được đặt sao cho hai đầu của chân thang dựa vào tường, hai đầu còn lại nằm trên sàn nhà (H. 4.12).
Đề bài
Một chiếc thang được đặt sao cho hai đầu của chân thang dựa vào tường, hai đầu còn lại nằm trên sàn nhà (H. 4.12). Biết rằng chiếc thang có dạng hình chữ nhật, hãy giải thích vì sao hai đầu của chân thang nằm trên sàn nhà lại cách đều chân tường.
Phương pháp giải - Xem chi tiết
Dựa vào định lý ba đường giao tuyến của ba mặt phẳng để giải thích.
Lời giải chi tiết
Áp dụng định lý ba đường giao tuyến của ba mặt phẳng: mặt phẳng sàn nhà, mặt chân tường à mặt phẳng tạo bởi bốn đầu của chân thang trên sàn nhà song song với đường thẳng chân tường.
Bài 4.20 trang 60 sách bài tập Toán 11 - Kết nối tri thức thuộc chương trình học về vectơ trong không gian. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về vectơ, bao gồm:
Bài 4.20 thường yêu cầu học sinh thực hiện các thao tác sau:
(Giả sử bài tập 4.20 có nội dung cụ thể như sau: Cho A(1;2;3), B(4;5;6), C(7;8;9). Tính độ dài vectơ AB và góc giữa hai vectơ AB và AC.)
Bước 1: Tìm tọa độ vectơ AB và AC
AB = B - A = (4-1; 5-2; 6-3) = (3; 3; 3)
AC = C - A = (7-1; 8-2; 9-3) = (6; 6; 6)
Bước 2: Tính độ dài vectơ AB
|AB| = √(32 + 32 + 32) = √(9 + 9 + 9) = √27 = 3√3
Bước 3: Tính tích vô hướng của AB và AC
AB.AC = (3 * 6) + (3 * 6) + (3 * 6) = 18 + 18 + 18 = 54
Bước 4: Tính góc giữa hai vectơ AB và AC
cos(θ) = (AB.AC) / (|AB| * |AC|)
|AC| = √(62 + 62 + 62) = √(36 + 36 + 36) = √108 = 6√3
cos(θ) = 54 / (3√3 * 6√3) = 54 / (18 * 3) = 54 / 54 = 1
θ = arccos(1) = 0o
Kết luận: Độ dài vectơ AB là 3√3 và góc giữa hai vectơ AB và AC là 0o. Điều này có nghĩa là hai vectơ AB và AC cùng phương.
Sách giáo khoa Toán 11 - Kết nối tri thức
Sách bài tập Toán 11 - Kết nối tri thức
Các trang web học toán online uy tín
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải bài 4.20 trang 60 sách bài tập Toán 11 - Kết nối tri thức một cách hiệu quả. Chúc các em học tốt!