Bài 7.35 trang 41 sách bài tập Toán 11 - Kết nối tri thức với cuộc sống là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải bài tập.
Cho hình lăng trụ \(ABC \cdot A'B'C'\) có \(A'B'C'\) và \(AA'C'\) là hai tam giác đều cạnh \(a\).
Đề bài
Cho hình lăng trụ \(ABC \cdot A'B'C'\) có \(A'B'C'\) và \(AA'C'\) là hai tam giác đều cạnh \(a\). Biết \(\left( {ACC'A'} \right) \bot \left( {A'B'C'} \right)\). Tính theo \(a\) thể tích khối lăng trụ \(ABC \cdot A'B'C'\).
Phương pháp giải - Xem chi tiết
Áp dụng công thức tính thể tích khối lăng trụ: \(S = B.h\).
Trong đó: \(B\) là diện tích đa giác đáy
\(h\) là đường cao của hình lăng trụ
Lời giải chi tiết
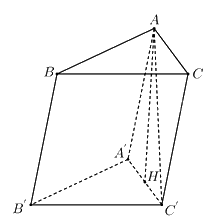
Kẻ \(AH \bot A'C'\) tại \(H\) thì \(AH \bot \left( {A'B'C'} \right)\).
Ta có \({S_{A'B'C'}} = \frac{{{a^2}\sqrt 3 }}{4};AH = \frac{{a\sqrt 3 }}{2}\)
Suy ra \({V_{ABC.A'B'C'}} = {S_{A'B'C'}} \cdot AH\)\( = \frac{{{a^2}\sqrt 3 }}{4} \cdot \frac{{a\sqrt 3 }}{2} = \frac{{3{a^3}}}{8}\).
Bài 7.35 trang 41 sách bài tập Toán 11 - Kết nối tri thức với cuộc sống là một bài toán ứng dụng thực tế, đòi hỏi học sinh phải hiểu rõ về đạo hàm và cách áp dụng đạo hàm để giải quyết các vấn đề liên quan đến tốc độ thay đổi của một đại lượng.
Trước khi đi vào giải bài, chúng ta cần phân tích kỹ đề bài để xác định rõ yêu cầu và các thông tin đã cho. Đề bài thường cung cấp một hàm số mô tả một quá trình nào đó, và yêu cầu tính đạo hàm của hàm số đó tại một điểm cụ thể, hoặc tìm điểm cực trị của hàm số.
Để giải bài 7.35 trang 41, học sinh cần nắm vững các kiến thức sau:
Dưới đây là lời giải chi tiết cho bài 7.35 trang 41 sách bài tập Toán 11 - Kết nối tri thức với cuộc sống. (Nội dung lời giải chi tiết sẽ được trình bày ở đây, bao gồm các bước giải, các công thức sử dụng, và các giải thích rõ ràng).
Ví dụ, nếu đề bài yêu cầu tính đạo hàm của hàm số f(x) = x2 + 2x - 1 tại x = 1, ta sẽ thực hiện như sau:
Ngoài bài 7.35, còn rất nhiều bài tập tương tự trong sách bài tập Toán 11 - Kết nối tri thức với cuộc sống. Các bài tập này thường yêu cầu học sinh vận dụng các kiến thức về đạo hàm để giải quyết các bài toán liên quan đến:
Để giải bài tập đạo hàm một cách hiệu quả, học sinh nên:
Bài 7.35 trang 41 sách bài tập Toán 11 - Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm và rèn luyện kỹ năng giải toán. Hy vọng với lời giải chi tiết và các hướng dẫn trên, các em học sinh sẽ tự tin hơn khi giải bài tập này và các bài tập tương tự.
| Công thức | Mô tả |
|---|---|
| f'(x) = limh→0 (f(x+h) - f(x))/h | Định nghĩa đạo hàm |
| (u + v)' = u' + v' | Quy tắc cộng |
| (u - v)' = u' - v' | Quy tắc trừ |