Bài 4.29 trang 67 sách bài tập Toán 11 thuộc chương trình Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về ứng dụng của đường thẳng và mặt phẳng trong không gian. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về vectơ, phương trình đường thẳng, phương trình mặt phẳng để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4.29 trang 67, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho hình bình hành ABCD. Qua A, B, C, D lần lượt vẽ bốn đường a, b, c, d đôi một song song và không nằm trong mặt phẳng (ABCD).
Đề bài
Cho hình bình hành ABCD. Qua A, B, C, D lần lượt vẽ bốn đường a, b, c, d đôi một song song và không nằm trong mặt phẳng (ABCD).
a) Chứng minh rằng hai mặt phẳng mp(a,b) và mp(c,d) song song với nhau.
b) Chứng minh rằng hai mặt phẳng mp(a,d) và mp(b,c) song song với nhau.
c) Một mặt phẳng cắt bốn đường thẳng a, b, c, d lần lượt tại A’, B’, C’, D’. Chứng minh rằng tứ giác A’B’C’D’ là hình bình hành.
Phương pháp giải - Xem chi tiết
Nếu mặt phẳng \(\left( \alpha \right)\) chứa hai đường thẳng cắt nhau và hai đường thẳng này song song với mặt phẳng \(\left( \beta \right)\) thì \(\left( \alpha \right)\) và \(\left( \beta \right)\) song song với nhau.
Lời giải chi tiết
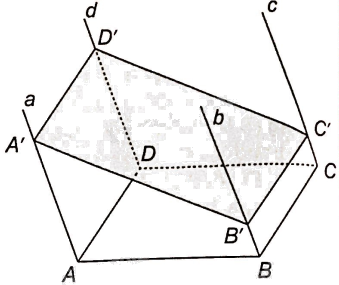
a) Vì a//d nên a//mp(c, d).
Vì ABCD là hình bình hành nên AB//CD, do đó AB// mp(c, d).
Mặt phẳng (a, b) chứa hai đường thẳng a và AB cắt nhau tại A và cùng song song với mp(c, d).
Do đó, hai mặt phẳng mp(a,b) và mp(c,d) song song với nhau.
b) Vì a//b nên a//mp(b, c).
Vì ABCD là hình bình hành nên AD//BC, do đó AD// mp(b, c).
Mặt phẳng (a, d) chứa hai đường thẳng a và AD cắt nhau tại A và cùng song song với mp(b, c).
hai mặt phẳng mp(a,d) và mp(b,c) song song với nhau.
c) Vì mặt phẳng (a, b) song song với mặt phẳng (c, d) nên giao tuyến của mặt phẳng (A’B’C’D’) với hai mặt phẳng đó song song với nhau, tức là A’B’//C’D’.
Vì hai mặt phẳng mp(a,d) và mp(b,c) song song với nhau nên giao tuyến của mặt phẳng (A’B’C’D’) với hai mặt phẳng đó song song với nhau, tức là A’D’//C’B’.
Tứ giác A’B’C’D’ có: A’B’//C’D’, A’D’//C’B’ nên tứ giác A’B’C’D’ là hình bình hành.
Bài 4.29 trang 67 sách bài tập Toán 11 Kết nối tri thức yêu cầu học sinh giải quyết một bài toán liên quan đến vị trí tương đối giữa đường thẳng và mặt phẳng trong không gian. Để giải bài toán này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản sau:
Đề bài: (Giả sử đề bài cụ thể của bài 4.29 được đưa ra ở đây. Ví dụ: Cho đường thẳng d: x = 1 + t, y = 2 - t, z = 3 + 2t và mặt phẳng (P): 2x - y + z = 5. Chứng minh rằng đường thẳng d nằm trên mặt phẳng (P).)
Lời giải:
Khi giải các bài tập về đường thẳng và mặt phẳng trong không gian, bạn cần chú ý những điều sau:
Bài 4.29 trang 67 sách bài tập Toán 11 Kết nối tri thức là một bài tập điển hình về ứng dụng của đường thẳng và mặt phẳng trong không gian. Việc nắm vững kiến thức và kỹ năng giải bài tập này sẽ giúp bạn tự tin hơn khi đối mặt với các bài toán tương tự trong kỳ thi và trong thực tế.