Bài 4.22 trang 63 sách bài tập Toán 11 - Kết nối tri thức là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ và ứng dụng của vectơ trong hình học để giải quyết các bài toán cụ thể.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4.22 trang 63, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng. Chứng minh rằng
Đề bài
Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng. Chứng minh rằng
a) CD//(ABEF)
b) EF//(ABCD)
c) CE//(ADF)
(Gợi ý: Theo SGK Bài 11, Luyện tập 3, ta đã biết CEFD là hình bình hành)
Phương pháp giải - Xem chi tiết
Nếu đường thẳng a không nằm trong mặt phẳng (P) và a song song với một đường thẳng nằm trong mặt phẳng (P) thì a song song với (P)
Lời giải chi tiết
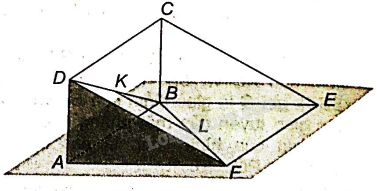
a) Vì ABCD là hình bình hành nên AB//CD, mà \(AB \subset \left( {ABEF} \right)\) nên CD//(ABEF)
b) Vì ABEF là hình bình hành nên EF//AB, mà \(AB \subset \left( {ABCD} \right)\) nên EF//(ABCD)
c) Vì CEFD là hình bình hành nên CE//DF, mà \(DF \subset \left( {ADF} \right)\) nên CE//(ADF)
Bài 4.22 trang 63 sách bài tập Toán 11 - Kết nối tri thức thuộc chương trình học về vectơ trong không gian. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về:
Bài 4.22 thường yêu cầu học sinh thực hiện các thao tác sau:
(Ở đây sẽ là lời giải chi tiết của bài tập 4.22, bao gồm các bước giải, giải thích rõ ràng và sử dụng các công thức liên quan. Ví dụ:)
Ví dụ: Cho hai điểm A(1; 2; 3) và B(4; 5; 6). Tìm tọa độ của vectơ AB.
Giải: Vectơ AB có tọa độ là (4-1; 5-2; 6-3) = (3; 3; 3).
Ngoài bài tập 4.22, học sinh có thể gặp các dạng bài tập tương tự như:
Để giải các bài tập về vectơ một cách hiệu quả, học sinh nên:
Học sinh có thể tham khảo thêm các tài liệu sau để hiểu rõ hơn về vectơ:
Bài 4.22 trang 63 sách bài tập Toán 11 - Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về vectơ. Hy vọng với lời giải chi tiết và các hướng dẫn trên, các em học sinh sẽ tự tin giải quyết bài tập này và đạt kết quả tốt trong môn Toán.