Bài 7.48 trang 42 sách bài tập Toán 11 thuộc chương trình học Toán 11 Kết nối tri thức với cuộc sống. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho lăng trụ tam giác đều ABC.A’B’C’ có tất cả các cạnh bằng a. Khoảng cách từ điểm A đến đường thẳng BB’ bằng.
Đề bài
Cho lăng trụ tam giác đều ABC.A’B’C’ có tất cả các cạnh bằng a. Khoảng cách từ điểm A đến đường thẳng BB’ bằng.
A. \(\frac{{a\sqrt 7 }}{2}\).
B. \(\frac{{a\sqrt {14} }}{4}\).
C. \(\frac{{a\sqrt 7 }}{4}\).
D. \(\frac{{a\sqrt {14} }}{2}\),
Lời giải chi tiết
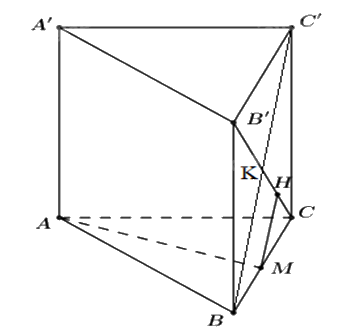
Gọi \(M\) là trung điểm \(BC\)
\(B'C \cap BC' = K\)
\(H\) là trung điểm \(KC\)
Do tứ giác \(BCC'B'\) là hình vuông suy ra \(B'C \bot BC';HM \bot B'C\,\,(1)\)
Dễ thấy \(AM \bot \left( {BCC'B'} \right) \Rightarrow AM \bot B'C{\kern 1pt} {\kern 1pt} \,\,\,(2)\)
Từ \(\left( 1 \right);\left( 2 \right) \Rightarrow \left( {AMH} \right) \bot B'C \Rightarrow AH \bot B'C\)
Từ đó suy ra khoảng cách từ điểm đến đường thẳng \(B'C\) bằng \(AH\)
Ta có \(AM = \frac{{a\sqrt 3 }}{2};HM = \frac{{BK}}{2} = \frac{{{\rm{a}}\sqrt 2 }}{4}\)
Xét tam giác \(AMH\) vuông tại \(M\) ta có \(AH = \sqrt {A{M^2} + H{M^2}} = \frac{{a\sqrt {14} }}{4}\)
Vậy, khoảng cách từ điểm đến đường thẳng \(B'C\) bằng \(\frac{{a\sqrt {14} }}{4}\)
Bài 7.48 trang 42 sách bài tập Toán 11 - Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc giải quyết các bài toán thực tế. Dưới đây là hướng dẫn chi tiết cách giải bài tập này:
Trước khi bắt đầu giải bài tập, chúng ta cần phân tích kỹ đề bài để xác định rõ yêu cầu và các thông tin đã cho. Bài 7.48 thường yêu cầu học sinh tìm đạo hàm của một hàm số, hoặc giải một phương trình, bất phương trình liên quan đến đạo hàm.
Để giải bài 7.48 trang 42 sách bài tập Toán 11, học sinh cần nắm vững các kiến thức sau:
(Nội dung lời giải chi tiết bài 7.48 sẽ được trình bày tại đây, bao gồm các bước giải cụ thể, giải thích rõ ràng và các lưu ý quan trọng. Ví dụ:)
Ví dụ: Giả sử bài 7.48 yêu cầu tìm đạo hàm của hàm số f(x) = x2 + 2x - 1.
Để củng cố kiến thức và kỹ năng giải bài tập về đạo hàm, học sinh có thể tham khảo các bài tập tương tự sau:
Khi giải bài tập về đạo hàm, học sinh cần lưu ý những điều sau:
Bài 7.48 trang 42 sách bài tập Toán 11 - Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm. Hy vọng với hướng dẫn chi tiết trên, các em học sinh sẽ tự tin giải bài tập này và đạt kết quả tốt trong môn Toán.
Giaitoan.edu.vn luôn đồng hành cùng các em học sinh trên con đường chinh phục môn Toán. Chúc các em học tập tốt!