Bài 1.42 trang 26 sách bài tập Toán 11 - Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Bài giải chi tiết dưới đây sẽ giúp các em hiểu rõ phương pháp giải và áp dụng vào các bài tập tương tự.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập toán 11.
Khẳng định nào sau đây đúng?
Đề bài
Khẳng định nào sau đây đúng?
A. Hàm số \(y = \cos x\) nghịch biến trên khoảng \(( - \pi ;0)\) và đồng biến trên khoảng \((0;\pi )\).
B. Hàm số \(y = \cos x\) đồng biến trên các khoảng \(( - \pi ;0)\) và \((0;\pi )\).
C. Hàm số \(y = \cos x\) nghịch biến trên các khoảng \(( - \pi ;0)\) và \((0;\pi )\).
D. Hàm số \(y = \cos x\) đồng biến trên khoảng \(( - \pi ;0)\) và nghịch biến trên khoảng \((0;\pi )\).
Phương pháp giải - Xem chi tiết
Dựa vào lý thuyết hàm số \(y = \cos x\) đồng biến trên khoảng \(\left( { - \pi + k2\pi ;k2\pi } \right)\) và nghịch biến trên khoảng \(\left( {k2\pi ;\pi + k2\pi } \right)\).
Hoặc dựa vào đồ thị hàm số để khẳng định tính đồng biến nghịch biến của nó.
Lời giải chi tiết
Đáp án D.
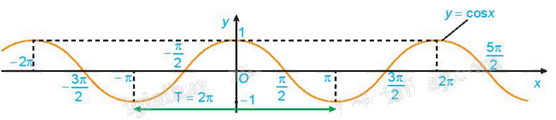
Dựa vào đồ thị, ta thấy hàm số \(y = \cos x\) đồng biến trên khoảng \(( - \pi ;0)\) và nghịch biến trên khoảng \((0;\pi )\).
Bài 1.42 trang 26 sách bài tập Toán 11 - Kết nối tri thức với cuộc sống yêu cầu học sinh khảo sát hàm số y = x3 - 3x2 + 2. Để giải bài này, chúng ta cần thực hiện các bước sau:
Thông qua việc giải bài 1.42 trang 26 sách bài tập Toán 11 - Kết nối tri thức với cuộc sống, học sinh đã nắm vững phương pháp khảo sát hàm số bằng đạo hàm, bao gồm việc xác định tập xác định, đạo hàm, điểm dừng, khoảng đồng biến, nghịch biến, cực trị, đạo hàm bậc hai, điểm uốn và vẽ đồ thị hàm số. Đây là một kỹ năng quan trọng trong chương trình Toán 11 và sẽ được áp dụng trong các bài học tiếp theo.
Để hiểu sâu hơn về ứng dụng của đạo hàm trong việc khảo sát hàm số, học sinh có thể tham khảo thêm các bài tập tương tự trong sách bài tập và sách giáo khoa Toán 11 - Kết nối tri thức với cuộc sống. Ngoài ra, các em cũng có thể tìm kiếm các tài liệu học tập trực tuyến và tham gia các khóa học toán online để nâng cao kiến thức và kỹ năng.
Xét hàm số y = x4 - 4x3 + 4x2 + 1. Hãy khảo sát hàm số này bằng phương pháp đạo hàm.
(Hướng dẫn giải: Thực hiện tương tự các bước như trong bài 1.42, bao gồm xác định tập xác định, đạo hàm, điểm dừng, khoảng đồng biến, nghịch biến, cực trị, đạo hàm bậc hai, điểm uốn và vẽ đồ thị hàm số.)
Khi giải các bài tập về khảo sát hàm số, học sinh cần chú ý đến việc xác định đúng tập xác định của hàm số và tính toán đạo hàm một cách chính xác. Ngoài ra, việc vẽ đồ thị hàm số cũng rất quan trọng để hình dung được hình dạng của hàm số và các đặc điểm của nó.
Giaitoan.edu.vn hy vọng rằng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải bài 1.42 trang 26 sách bài tập Toán 11 - Kết nối tri thức với cuộc sống và đạt kết quả tốt trong môn Toán.