Bài 7.25 trang 35 sách bài tập Toán 11 thuộc chương trình Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Hãy cùng khám phá lời giải chi tiết của bài 7.25 ngay sau đây!
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\)
Đề bài
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\), tam giác \(SAD\) đều và nằm trong mặt phẳng vuông góc với mặt đáy \(\left( {ABCD} \right)\). Gọi \(H,M\) lần lượt là trung điểm của các cạnh \(AD\) và \(AB\).
a) Tính côsin của góc giữa đường thẳng \(SC\) và mặt đáy \(\left( {ABCD} \right)\).
b) Chứng minh rằng \(\left( {SMD} \right) \bot \left( {SHC} \right)\).
Phương pháp giải - Xem chi tiết
Áp dụng tính chất:
\(\left\{ \begin{array}{l}\left( P \right) \bot \left( Q \right)\\a \subset \left( P \right)\\b = \left( P \right) \cap \left( Q \right)\\a \bot b\end{array} \right. \Rightarrow a \bot \left( Q \right)\)
Ta có \(\left( {SAD} \right) \bot \left( {ABCD} \right)\) và \(SH \bot AD\) nên \(SH \bot \left( {ABCD} \right)\),
Xác định hình chiếu của đường thẳng \(SC\) và mặt phẳng \(\left( {ABCD} \right)\)
Tính góc giữa hai đường thẳng \({\rm{SC}}\) và hình chiếu của nó rồi kết luận
Để chứng minh \(\left( {SDM} \right) \bot \left( {SCH} \right)\) sử dụng tính chất \(DM \bot CH,DM \bot SH\)
Lời giải chi tiết
a) Ta có \(\left( {SAD} \right) \bot \left( {ABCD} \right)\) và \(SH \bot AD\) nên \(SH \bot \left( {ABCD} \right)\), suy ra góc giữa đường thẳng \(SC\) và mặt phẳng \(\left( {ABCD} \right)\) bằng góc giữa hai đường thẳng \({\rm{SC}}\) và \({\rm{CH}}\), mà \(\left( {{\rm{SC}},{\rm{CH}}} \right) = \widehat {{\rm{SCH}}}\), ta tính được \(SH = \frac{{a\sqrt 3 }}{2},HC = \frac{{a\sqrt 5 }}{2}\) và \(SC = a\sqrt 2 \).
Do đó \({\rm{cos}}\widehat {SHC} = \frac{{HC}}{{SC}} = \frac{{\sqrt {10} }}{4}\).
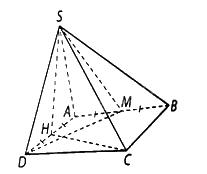
b) Ta có \(DM \bot CH,DM \bot SH\) nên \(DM \bot \left( {SCH} \right)\). Hơn nữa, mặt phẳng (SDM) chứa đường thẳng \(DM\) nên \(\left( {SDM} \right) \bot \left( {SCH} \right)\).
Bài 7.25 trang 35 sách bài tập Toán 11 - Kết nối tri thức với cuộc sống yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết một bài toán thực tế liên quan đến việc tối ưu hóa. Để giải bài toán này một cách hiệu quả, chúng ta cần thực hiện các bước sau:
Đầu tiên, cần xác định rõ hàm số biểu diễn đại lượng cần tối ưu hóa. Trong bài toán này, hàm số có thể là biểu thức tính diện tích, chi phí, lợi nhuận, hoặc bất kỳ đại lượng nào khác mà bài toán yêu cầu.
Xác định tập xác định của hàm số là bước quan trọng để đảm bảo rằng các giá trị của biến số nằm trong phạm vi cho phép. Tập xác định có thể bị giới hạn bởi các điều kiện thực tế của bài toán.
Tính đạo hàm cấp một của hàm số để tìm các điểm cực trị. Đạo hàm cấp một cho biết tốc độ thay đổi của hàm số tại một điểm nhất định.
Giải phương trình đạo hàm cấp một bằng 0 để tìm các điểm cực trị. Các điểm cực trị là các điểm mà tại đó hàm số đạt giá trị lớn nhất hoặc nhỏ nhất cục bộ.
Sử dụng dấu của đạo hàm cấp một để xác định loại cực trị (cực đại hoặc cực tiểu). Nếu đạo hàm đổi dấu từ dương sang âm tại một điểm, thì điểm đó là cực đại. Nếu đạo hàm đổi dấu từ âm sang dương, thì điểm đó là cực tiểu.
Kiểm tra giá trị của hàm số tại các điểm biên của tập xác định để tìm giá trị lớn nhất hoặc nhỏ nhất tuyệt đối của hàm số.
Giả sử bài toán yêu cầu tìm kích thước của một mảnh đất hình chữ nhật có diện tích cố định sao cho chu vi nhỏ nhất. Ta có thể giải bài toán này như sau:
Giải bài 7.25 trang 35 sách bài tập Toán 11 - Kết nối tri thức với cuộc sống đòi hỏi học sinh phải nắm vững kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc giải quyết các bài toán tối ưu hóa. Bằng cách thực hiện các bước trên một cách cẩn thận và chính xác, các em học sinh có thể tự tin giải quyết các bài toán tương tự.
Hy vọng với lời giải chi tiết và hướng dẫn giải trên, các em học sinh sẽ hiểu rõ hơn về bài 7.25 và có thể áp dụng kiến thức này vào việc giải các bài tập khác. Chúc các em học tập tốt!