Bài 4.51 trang 72 sách bài tập Toán 11 - Kết nối tri thức với cuộc sống là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về đường thẳng và mặt phẳng trong không gian để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
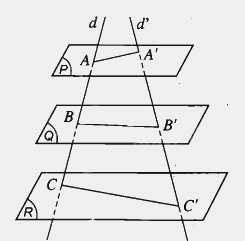
Cho ba mặt phẳng (P), (Q), (R) đôi một song song với nhau. Đường thẳng d cắt các mặt phẳng (P), (Q), (R) lần lượt tại A, B, C.
Đề bài
Cho ba mặt phẳng (P), (Q), (R) đôi một song song với nhau. Đường thẳng d cắt các mặt phẳng (P), (Q), (R) lần lượt tại A, B, C. Đường thẳng d’ cắt các mặt phẳng (P), (Q), (R) lần lượt tại A’, B’, C’. Biết rằng \(\frac{{AB}}{{AC}} = \frac{2}{3}\), tỉ số \(\frac{{A'B'}}{{A'C'}}\) bằng
A. \(\frac{1}{3}\)
B. \(\frac{2}{3}\)
C. \(\frac{3}{2}\)
D. \(\frac{1}{2}\).
Phương pháp giải - Xem chi tiết
Định lí Thalès trong không gian: Ba mặt phẳng đôi một song song chắn hai cát tuyến phân biệt bất kì những đoạn thẳng tỉ lệ.
Lời giải chi tiết
Đáp án B.
Áp dụng định lí Thalès cho ba mặt phẳng đôi một song song (P), (Q), (R) và hai cát tuyến d, d’ ta có: \(\frac{{A'B'}}{{A'C'}} = \frac{{AB}}{{AC}} = \frac{2}{3}\)
Bài 4.51 trang 72 sách bài tập Toán 11 - Kết nối tri thức với cuộc sống là một bài toán thuộc chương trình hình học không gian, cụ thể là phần về đường thẳng và mặt phẳng. Để giải bài toán này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản như:
Trước khi bắt tay vào giải bài toán, chúng ta cần đọc kỹ đề bài và phân tích các yếu tố quan trọng. Xác định rõ các đường thẳng, mặt phẳng được đề cập trong bài và mối quan hệ giữa chúng. Sau đó, tìm kiếm các dữ kiện đã cho và các yêu cầu cần tìm.
Thông thường, bài toán sẽ yêu cầu chúng ta chứng minh một mối quan hệ nào đó giữa đường thẳng và mặt phẳng, hoặc tìm một điểm thuộc đường thẳng hoặc mặt phẳng thỏa mãn một điều kiện nhất định.
Để cung cấp lời giải chi tiết, chúng ta cần xem xét cụ thể nội dung của bài toán. Tuy nhiên, dựa trên kinh nghiệm giải các bài toán tương tự, chúng ta có thể đưa ra một số bước giải chung:
Giả sử bài toán yêu cầu chứng minh một đường thẳng song song với một mặt phẳng. Chúng ta có thể sử dụng các phương pháp sau:
Khi giải bài toán về đường thẳng và mặt phẳng, chúng ta cần lưu ý một số điều sau:
Bài toán về đường thẳng và mặt phẳng có nhiều ứng dụng trong thực tế, chẳng hạn như:
Bài 4.51 trang 72 sách bài tập Toán 11 - Kết nối tri thức với cuộc sống là một bài toán quan trọng giúp học sinh củng cố kiến thức về đường thẳng và mặt phẳng trong không gian. Bằng cách nắm vững các kiến thức cơ bản và áp dụng các phương pháp giải toán phù hợp, chúng ta có thể giải quyết bài toán này một cách hiệu quả.
Hy vọng rằng, với hướng dẫn chi tiết này, các bạn học sinh sẽ tự tin hơn khi đối mặt với bài toán này và các bài toán tương tự trong tương lai.