Bài 7.2 trang 26 sách bài tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc tìm cực trị của hàm số. Bài tập này yêu cầu học sinh phải nắm vững kiến thức về các quy tắc tính đạo hàm và cách xác định điểm cực trị của hàm số.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 7.2 trang 26 sách bài tập Toán 11 Kết nối tri thức, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho hình hộp có tất cả các cạnh bằng nhau và góc bằng .
Đề bài
Cho hình hộp ABCD có tất cả các cạnh bằng nhau và góc A’AD bằng 120 độ. Tính góc giữa các cặp đường thẳng sau: A’C và BD, AD và BB’, A’D và BB’.
Phương pháp giải - Xem chi tiết
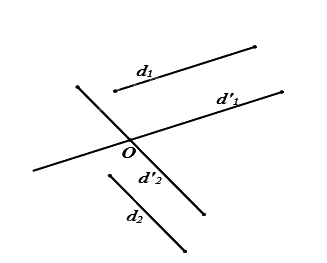
Từ \(O\) dựng các đường thẳng \(d'_1,d'_2\) lần lượt song song có thể trùng nếu \(O\) nằm trên một trong hai đường thẳngvới \({d_1}\) và \({d_2}\). Góc giữa hai đường thẳng \(d'_1,d'_2\)chính là góc giữa hai đường thẳng\({d_1},{d_2}\).
Lưu ý: Hai đường chéo của hình thoi hoặc hình vuông thì vuông góc với nhau.
Lời giải chi tiết
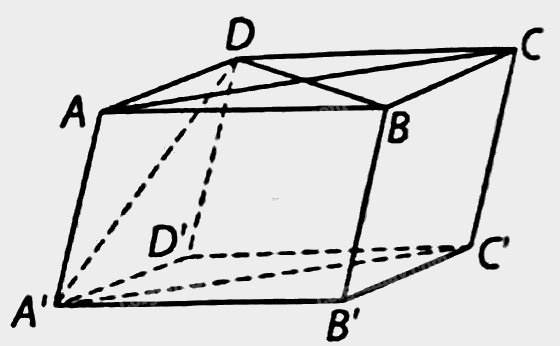
Vì ABCD là hình thoi và A’C’ // AC nên \((A’C’, BD) = (AC, BD) = 90^o\).
Vì BB’ // AA’ nên \((AD, BB’) = (AD, AA’) = 180^o - \widehat {AA'D} = 60^o \) và \(\left( {A'D, BB'} \right) = \left( {A'D,AA'} \right) = \widehat {AA'D} = 30^o\).
Bài 7.2 trang 26 sách bài tập Toán 11 Kết nối tri thức yêu cầu học sinh giải quyết một bài toán thực tế liên quan đến việc tối ưu hóa một hàm số. Để giải bài toán này, học sinh cần áp dụng các kiến thức về đạo hàm, điểm cực trị và các ứng dụng của đạo hàm trong thực tế.
Trước khi bắt đầu giải bài toán, chúng ta cần phân tích kỹ đề bài để xác định rõ các yếu tố quan trọng như hàm số cần tối ưu hóa, miền xác định của hàm số và điều kiện ràng buộc (nếu có). Việc phân tích bài toán một cách cẩn thận sẽ giúp chúng ta lựa chọn phương pháp giải phù hợp và tránh được những sai sót không đáng có.
Giả sử chúng ta có hàm số f(x) = x3 - 3x2 + 2. Để tìm cực trị của hàm số này, chúng ta thực hiện các bước sau:
Khi giải bài toán về cực trị của hàm số, cần lưu ý một số điểm sau:
Bài toán về cực trị của hàm số có nhiều ứng dụng thực tế trong các lĩnh vực khác nhau như kinh tế, kỹ thuật, vật lý,... Ví dụ, trong kinh tế, bài toán này có thể được sử dụng để tìm ra mức sản lượng tối ưu để đạt được lợi nhuận cao nhất. Trong kỹ thuật, bài toán này có thể được sử dụng để thiết kế các cấu trúc có độ bền cao nhất. Trong vật lý, bài toán này có thể được sử dụng để tìm ra quỹ đạo của một vật thể chuyển động dưới tác dụng của trọng lực.
Để rèn luyện kỹ năng giải bài toán về cực trị của hàm số, bạn có thể làm thêm các bài tập tương tự trong sách bài tập Toán 11 Kết nối tri thức hoặc trên các trang web học toán online.
Bài 7.2 trang 26 sách bài tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh nắm vững kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc tìm cực trị của hàm số. Hy vọng rằng với hướng dẫn chi tiết và dễ hiểu trên đây, các em học sinh sẽ tự tin giải bài tập và đạt kết quả tốt trong môn Toán.