Bài 7.24 trang 34 sách bài tập Toán 11 Kết nối tri thức là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về đường thẳng và mặt phẳng trong không gian để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 7.24 trang 34, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh a
Đề bài
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh a, biết \(\left( {SAB} \right) \bot \left( {ABCD} \right)\), \(\left( {SAD} \right) \bot \left( {ABCD} \right)\) và \(SA = a\). Tính côsin của số đo góc nhị diện \(\left[ {S,BD,C} \right]\) và góc nhị diện \(\left[ {B,SC,D} \right]\).
Phương pháp giải - Xem chi tiết
Để tính góc giữa hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) ta có thể thực hiện cách sau:
Tìm hai đường thẳng \(a,b\) lần lượt vuông góc với hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\).
Khi đó góc giữa hai đường thẳng \(a,b\) chính là góc giữa hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\).
\(\left\{ \begin{array}{l}a \bot \left( \alpha \right)\\b \bot \left( \beta \right)\end{array} \right. \Rightarrow \widehat {\left( {\left( \alpha \right),\left( \beta \right)} \right)} = \widehat {\left( {a,b} \right)}\).
Áp dụng tính chất: Hình vuông có hai đường chéo vuông góc
Dựa vào tỉ số lượng giác trong tam giác vuông để tìm góc
Áp dụng định lí côsin trong tam giác
Lời giải chi tiết
Ta có \(SO \bot BD,CO \bot BD\) nên góc nhị diện \(\left[ {S,BD,C} \right]\) bằng \(\widehat {SOC}\).
Vì tam giác \(SAO\) vuông tại \(A\) nên \(SO = \sqrt {S{A^2} + A{O^2}} = \frac{{a\sqrt 6 }}{2}\) và \({\rm{cos}}\widehat {SOC} = - {\rm{cos}}\widehat {SOA} = - \frac{{OA}}{{SO}} = - \frac{{\sqrt 3 }}{3}\).
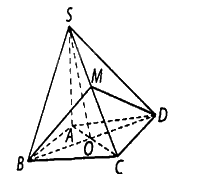
Kẻ \(BM \bot SC\) tại \(M\) thì \(DM \bot SC\) nên \(\left[ {B,SC,D} \right] = \widehat {BMD}\).
Ta có \(BC \bot \left( {SAB} \right)\) nên tam giác \(SBC\) vuông tại \(B\), tính được \(SB = a\sqrt 2 \), \(SC = a\sqrt 3 \) và \(DM = BM = \frac{{SB \cdot BC}}{{SC}} = \frac{{a\sqrt 6 }}{3}\).
Áp dụng định lí côsin trong tam giác \(BDM\), ta có: \({\rm{cos}}\widehat {BMD} = \frac{{B{M^2} + D{M^2} - B{D^2}}}{{2 \cdot BM \cdot DM}} = - \frac{3}{4}\).
Bài 7.24 trang 34 sách bài tập Toán 11 Kết nối tri thức yêu cầu chúng ta xét vị trí tương đối giữa đường thẳng và mặt phẳng. Để giải bài toán này, chúng ta cần nắm vững các kiến thức cơ bản về:
Trước khi đi vào giải chi tiết, chúng ta cần phân tích bài toán để xác định rõ yêu cầu và các dữ kiện đã cho. Thông thường, bài toán sẽ cung cấp thông tin về vị trí của các điểm, đường thẳng và mặt phẳng trong không gian. Dựa vào đó, chúng ta sẽ sử dụng các kiến thức đã học để suy luận và tìm ra kết quả.
(Nội dung lời giải chi tiết bài 7.24 trang 34 sẽ được trình bày tại đây. Bao gồm các bước giải, các công thức sử dụng và giải thích rõ ràng từng bước. Ví dụ:)
Ví dụ: Giả sử bài toán yêu cầu chứng minh đường thẳng d song song với mặt phẳng (P). Chúng ta sẽ thực hiện các bước sau:
Sau khi thực hiện đầy đủ các bước, chúng ta sẽ kết luận rằng đường thẳng d song song với mặt phẳng (P).
Ngoài bài 7.24, sách bài tập Toán 11 Kết nối tri thức còn có nhiều bài tập tương tự về vị trí tương đối giữa đường thẳng và mặt phẳng. Để nắm vững kiến thức, các em nên luyện tập thêm các bài tập sau:
Để giải các bài tập về vị trí tương đối giữa đường thẳng và mặt phẳng một cách hiệu quả, các em có thể tham khảo một số mẹo sau:
Bài 7.24 trang 34 sách bài tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp các em củng cố kiến thức về vị trí tương đối giữa đường thẳng và mặt phẳng. Hy vọng với lời giải chi tiết và các mẹo giải bài tập mà Giaitoan.edu.vn cung cấp, các em sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong môn Toán.
| Công thức | Mô tả |
|---|---|
| d // (P) | Đường thẳng d song song với mặt phẳng (P) |
| d ⊥ (P) | Đường thẳng d vuông góc với mặt phẳng (P) |
| φ | Góc giữa đường thẳng d và mặt phẳng (P) |