Bài 7.28 trang 38 sách bài tập Toán 11 - Kết nối tri thức là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 7.28 trang 38, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh \(a\). \(SA \bot \left( {ABC} \right)\) và \(SA = 2a\)
Đề bài
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh \(a\). \(SA \bot \left( {ABC} \right)\) và \(SA = 2a\)
Tính theo \(a\) khoảng cách
a) Từ điểm \(B\) đến mặt phẳng \(\left( {SAC} \right)\).
b) Từ điểm \(A\) đến mặt phẳng \(\left( {SBC} \right)\).
c) Giữa hai đường thẳng \(AB\) và \(SC\).
Phương pháp giải - Xem chi tiết
a) Từ điểm \(B\) đến mặt phẳng \(\left( {SAC} \right)\).
Bước 1: Xác định hình chiếu vuông góc của lên mặt phẳng là \(H\)
Bước 2: Tính \(BH\).
a) Tính khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( {SBC} \right)\).
Bước 1: Xác định hình chiếu vuông góc của \(A\) lên mặt phẳng \(\left( {SBC} \right)\) là \(K\)
Bước 2: Tính \(AK\).
c) Tính khoảng cách từ giữa hai đường thẳng \(AB\) và \(SC\).
Bước 1: Dựng mặt phẳng \(\left( {SCD} \right)\) chứa \(SC\) và song song với \(AB\)
Dựng hình bình hành \(ABCD\) thì \(AB//\left( {SCD} \right)\) và mặt phẳng \(\left( {SCD} \right)\) chứa \(SC\) nên \(d\left( {AB,SC} \right) = d\left( {AB,\left( {SCD} \right)} \right)\). Mà \(d\left( {AB,\left( {SCD} \right)} \right) = d\left( {A,\left( {SCD} \right)} \right)\)
Bước 2: Tính \(d\left( {A,\left( {SCD} \right)} \right)\).
Kết luận \(d\left( {AB,SC} \right)\).
Lời giải chi tiết
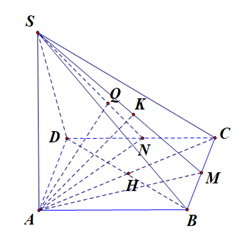
a) Kẻ \(BH \bot AC\) tại \(H\), mà \(SA \bot \left( {ABC} \right)\) nên \(SA \bot BH\), suy ra \(BH \bot \left( {SAC} \right)\).
Do đó, \(d\left( {B,\left( {SAC} \right)} \right) = BH = \frac{{a\sqrt 3 }}{2}\).
b) Kẻ \(AM \bot BC\) tại \(M\) và \(AK \bot SM\) tại \(K\) thì \(AK \bot \left( {SBC} \right)\), suy ra \(d\left( {A,\left( {SBC} \right)} \right) = AK\).
Ta có: \(\frac{1}{{A{K^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{M^2}}} = \frac{{19}}{{12{a^2}}} \Rightarrow AK = 2{\rm{a}}\sqrt {\frac{3}{{19}}} \). Nên \(d\left( {A,\left( {SBC} \right)} \right) = 2{\rm{a}}\sqrt {\frac{3}{{19}}} \).
c) Dựng hình bình hành \(ABCD\) thì \(AB\parallel \left( {SCD} \right)\) và mặt phẳng \(\left( {SCD} \right)\) chứa \(SC\) nên\(d\left( {AB,SC} \right) = d\left( {AB,\left( {SCD} \right)} \right)\).
Mà \(d\left( {AB,\left( {SCD} \right)} \right) = d\left( {A,\left( {SCD} \right)} \right)\), tính tương tự câu b) ta được
\(d\left( {A,\left( {SCD} \right)} \right) = 2{\rm{a}}\sqrt {\frac{3}{{19}}} \). Vậy \(d\left( {AB,SC} \right) = 2{\rm{a}}\sqrt {\frac{3}{{19}}} \).
Bài 7.28 trang 38 sách bài tập Toán 11 - Kết nối tri thức thuộc chương trình học về đạo hàm của hàm số. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về đạo hàm, bao gồm:
Bài tập 7.28 thường yêu cầu học sinh thực hiện các thao tác sau:
Để giải bài 7.28 trang 38, chúng ta sẽ tiến hành theo các bước sau:
Ví dụ, giả sử bài tập yêu cầu tính đạo hàm của hàm số f(x) = x2 + 2x + 1 tại điểm x = 0. Chúng ta sẽ thực hiện như sau:
Vậy, đạo hàm của hàm số f(x) tại điểm x = 0 là 2.
Ngoài bài 7.28, còn rất nhiều bài tập tương tự trong sách bài tập Toán 11 - Kết nối tri thức. Để giải các bài tập này, học sinh cần luyện tập thường xuyên và nắm vững các kiến thức cơ bản về đạo hàm. Một số dạng bài tập thường gặp bao gồm:
Để học tốt môn Toán 11, đặc biệt là phần đạo hàm, học sinh nên:
Bài 7.28 trang 38 sách bài tập Toán 11 - Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm. Hy vọng với lời giải chi tiết và hướng dẫn cụ thể trên đây, các em học sinh sẽ tự tin hơn khi giải bài tập và đạt kết quả tốt trong môn Toán.
| Công thức | Mô tả |
|---|---|
| (u + v)' = u' + v' | Đạo hàm của tổng |
| (u - v)' = u' - v' | Đạo hàm của hiệu |
| (uv)' = u'v + uv' | Đạo hàm của tích |