Bài 7.4 trang 26 sách bài tập Toán 11 - Kết nối tri thức là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ và ứng dụng của vectơ trong hình học để giải quyết các bài toán cụ thể.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 7.4 trang 26, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho hình chóp \(S.ABCD\) có đáy là hình vuông tâm \(O\) và tất cả các cạnh của hình chóp đều bằng a.
Đề bài
Cho hình chóp \(S.ABCD\) có đáy là hình vuông tâm \(O\) và tất cả các cạnh của hình chóp đều bằng a. Gọi \(M\), N lần lượt là trung điểm các cạnh \(SA,AB\)
a) Tính góc giữa các cặp đường thẳng sau: \(MN\) và \(SD;MO\) và \(SB\)
b) Tính tang của góc giữa hai đường thẳng \(SN\) và \(BC\).
Phương pháp giải - Xem chi tiết
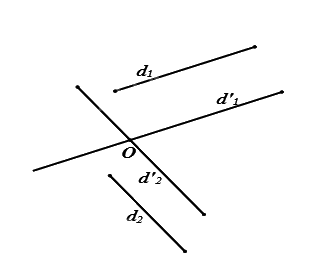
Từ \(O\) dựng các đường thẳng \(d'_1,d'_2\) lần lượt song song có thể trùng nếu \(O\) nằm trên một trong hai đường thẳngvới \({d_1}\) và \({d_2}\). Góc giữa hai đường thẳng \(d'_1,d'_2\)chính là góc giữa hai đường thẳng\({d_1},{d_2}\).
Lưu ý :
Áp dụng định lý Pytago đảo để chứng minh tam giác vuông
Áp dụng tính chất đường trung bình tam giác
Áp dụng tính chất \(\left\{ \begin{array}{l}a//b\\a \bot c\end{array} \right. \Rightarrow b \bot c\)
Lời giải chi tiết
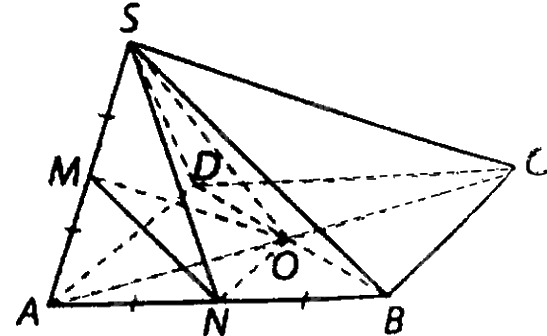
a) Ta có: \(B{D^2} = S{B^2} + S{D^2} = 2{a^2}\) nên \(\Delta SBD\) vuông tại \(S\), mà \(MN//SB\), suy ra \(\left( {MN,SD} \right) = \left( {SB,SD} \right) = {90^ \circ }\).
Với O là giao điểm của \(AC\) và \(BD\) thì \(MO//SC\).
Khi đó \(\left( {MO,SB} \right) = \left( {SC,SB} \right) = \widehat {BSC} = {60^ \circ }\).
b) Vì \(ON{\rm{ }}//BC\) nên \(\left( {SN,BC} \right) = \left( {SN,ON} \right) = \widehat {SNO}\).
Ta có \(SO = \frac{{a\sqrt 2 }}{2};ON = \frac{a}{2}\) và tam giác \(SNO\)vuông tại O nên \({\rm{tan}}\widehat {SNO} = \frac{{SO}}{{ON}} = \sqrt 2 \).
Vậy \({\rm{tan}}\left( {SN,BC} \right) = \sqrt 2 \).
Bài 7.4 trang 26 sách bài tập Toán 11 - Kết nối tri thức thuộc chương trình học về vectơ trong không gian. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về:
Bài tập 7.4 thường bao gồm các dạng bài sau:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài tập 7.4 trang 26, chúng ta sẽ đi vào giải chi tiết từng phần của bài tập. (Nội dung giải chi tiết sẽ được trình bày ở đây, bao gồm các bước giải, giải thích rõ ràng và ví dụ minh họa. Ví dụ:)
Cho A(1; 2; 3), B(4; 5; 6). Tìm tọa độ của vectơ AB.
Giải:
Vectơ AB có tọa độ là: AB = (4 - 1; 5 - 2; 6 - 3) = (3; 3; 3).
Ngoài bài tập 7.4, các em có thể gặp các bài tập tương tự với các yêu cầu khác nhau. Để giải quyết các bài tập này, các em cần:
Để học tốt môn Toán 11, đặc biệt là phần vectơ, các em nên:
Bài 7.4 trang 26 sách bài tập Toán 11 - Kết nối tri thức là một bài tập quan trọng giúp các em củng cố kiến thức về vectơ. Hy vọng với lời giải chi tiết và hướng dẫn giải bài tập mà Giaitoan.edu.vn cung cấp, các em sẽ học tốt môn Toán 11 và đạt kết quả cao trong các kỳ thi.
| Công thức vectơ quan trọng | Mô tả |
|---|---|
| AB = B - A | Vectơ AB được tính bằng hiệu tọa độ của điểm B trừ điểm A. |
| a.b = |a||b|cos(θ) | Tích vô hướng của hai vectơ a và b. |