Bài 7.40 trang 41 sách bài tập Toán 11 - Kết nối tri thức với cuộc sống là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải bài tập một cách hiệu quả.
Người ta cắt bỏ bốn hình vuông cùng kích thước ở bốn góc của một tấm tôn hình vuông có cạnh \(1{\rm{\;m}}\)
Đề bài
Người ta cắt bỏ bốn hình vuông cùng kích thước ở bốn góc của một tấm tôn hình vuông có cạnh \(1{\rm{\;m}}\) để gò lại thành một chiếc thùng có dạng hình hộp chữ nhật không nắp. Hỏi cạnh của các hình vuông cần bỏ đi có độ dài bằng bao nhiêu để thùng hình hộp nhận được có thể tích lớn nhất?
Phương pháp giải - Xem chi tiết
Áp dụng công thức tính thể tích khối hộp chữ nhật: \({\rm{V}} = a.b.c\).
Trong đó: \(a,b,c\) là độ dài 3 cạnh hình hộp chữ nhật có chung 1 đỉnh
Bước 1: Gọi \(x\left( {{\rm{\;m}}} \right)\) là chiều dài cạnh hình vuông nhỏ tại mỗi góc của tấm tôn được cắt bỏ đi (với \(0 < x < \frac{1}{2}\) ).
Tính thể tích hình hộp chữ nhật nhận được
Bước 2: Tìm giá trị lớn nhất của thể tích hình hộp chữ nhật nhận được
Từ đó tìm \(x\)
Lời giải chi tiết
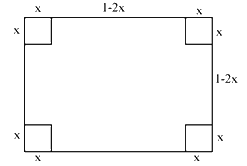
Gọi \(x\left( {{\rm{\;m}}} \right)\) là chiều dài cạnh hình vuông nhỏ tại mỗi góc của tấm tôn được cắt bỏ đi (với \(0 < x < \frac{1}{2}\) ).
Thể tích hình hộp chữ nhật nhận được là
\(V = {(1 - 2x)^2} \cdot x = \frac{1}{4} \cdot \left( {1 - 2x} \right) \cdot \left( {1 - 2x} \right) \cdot 4x \le \frac{1}{4} \cdot {\left( {\frac{{1 - 2x + 1 - 2x + 4x}}{3}} \right)^3} = \frac{2}{{27}}\)
Dấu "=" xảy ra khi \(1 - 2x = 4x \Leftrightarrow x = \frac{1}{6}\).
Vậy để thể tích chiếc thùng là lớn nhất thì các cạnh của hình vuông được cắt bỏ đi là \(\frac{1}{6}{\rm{\;m}}\).
Bài 7.40 trang 41 sách bài tập Toán 11 - Kết nối tri thức với cuộc sống thuộc chương trình học Toán 11, tập trung vào ứng dụng của đạo hàm trong việc giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh phải hiểu rõ các khái niệm về đạo hàm, quy tắc tính đạo hàm và cách sử dụng đạo hàm để tìm cực trị, khoảng đơn điệu của hàm số.
Trước khi bắt đầu giải bài tập, điều quan trọng nhất là phải đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Trong bài 7.40, học sinh cần xác định hàm số, tìm đạo hàm của hàm số đó và sau đó sử dụng đạo hàm để giải quyết các vấn đề được đặt ra trong đề bài.
Giả sử đề bài yêu cầu tìm cực trị của hàm số f(x) = x3 - 3x2 + 2.
Đạo hàm có rất nhiều ứng dụng trong thực tế, chẳng hạn như:
Để củng cố kiến thức, bạn có thể làm thêm các bài tập tương tự trong sách bài tập Toán 11 - Kết nối tri thức với cuộc sống. Ngoài ra, bạn cũng có thể tìm kiếm các bài tập trực tuyến trên các trang web học toán.
Giải bài 7.40 trang 41 sách bài tập Toán 11 - Kết nối tri thức với cuộc sống đòi hỏi học sinh phải nắm vững kiến thức về đạo hàm và các quy tắc tính đạo hàm. Bằng cách thực hành thường xuyên và áp dụng các kiến thức đã học vào giải quyết các bài toán thực tế, học sinh có thể nâng cao kỹ năng giải toán và đạt kết quả tốt trong môn Toán.