Bài 4.13 trang 59 sách bài tập Toán 11 Kết nối tri thức là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ và ứng dụng của vectơ trong hình học để giải quyết các bài toán cụ thể.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4.13 trang 59, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho tứ diện ABCD. Gọi M, N, P lần lượt là các điểm thuộc các cạnh AB, BC, CD.
Đề bài
Cho tứ diện ABCD. Gọi M, N, P lần lượt là các điểm thuộc các cạnh AB, BC, CD. Xác định giao điểm của đường thẳng AD và mặt phẳng (MNP) trong các trường hợp sau:
a, Đường thẳng NP song song với đường thẳng BD.
b, Đường thẳng NP cắt BD.
Phương pháp giải - Xem chi tiết
Dựa vào định lý về 3 đường giao tuyến của 3 mặt phẳng: Nếu có 2 giao tuyến của song song với nhau thì giao tuyến thứ 3 cũng song song với 2 giao tuyến đó. Còn nếu có 2 giao tuyến cắt nhau thì 3 giao tuyến đó đồng quy.
Lời giải chi tiết
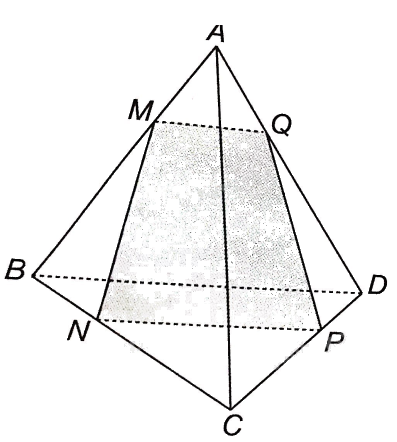
a,
NP là giao tuyến của hai mặt phẳng (MNP và (BCD
BD là giao tuyến của hai mặt phẳng (ABD và (BCD
Mà NP // BD nên giao tuyến của (MNP và (ABD cũng là một đường thẳng song song với NP và BD.
Ta thấy M thuộc AB nên M là điểm chung của (MNP và (ABD.
Vậy giao tuyến của (MNP và (ABD là đường thẳng d đi qua M, song song với NP và BD.
Trong mặt phẳng (ABD, gọi Q là giao điểm giữa d và AD.
Vậy giao điểm của đường thẳng AD và mặt phẳng (MNP chính là điểm Q.
b,
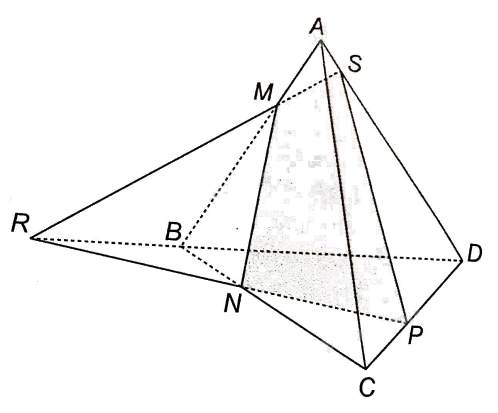
NP là giao tuyến của hai mặt phẳng (MNP) và (BCD)
BD là giao tuyến của hai mặt phẳng (ABD) và (BCD)
Mà đường thẳng NP và BD cắt nhau nên giao tuyến d của (MNP) và (ABD) là một đường thẳng đồng quy với NP và BD. (gọi R là giao điểm của NP và BD, vậy d đi qua điểm R
Ta thấy M thuộc AB nên M là điểm chung của (MNP) và (ABD). Vậy M thuộc đường giao tuyến d.
Trong mặt phẳng (BCD) gọi S là giao điểm của MR và BD, vậy giao tuyến d cũng sẽ đi qua điểm S.
Vậy giao điểm của đường thẳng AD và mặt phẳng (MNP) chính là điểm S.
Bài 4.13 trang 59 sách bài tập Toán 11 Kết nối tri thức yêu cầu chúng ta giải quyết một bài toán liên quan đến vectơ trong không gian. Để giải bài toán này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về vectơ, bao gồm:
Trước khi đi vào giải bài toán cụ thể, chúng ta cần đọc kỹ đề bài, xác định rõ các yếu tố đã cho và yêu cầu của bài toán. Thông thường, bài toán sẽ cung cấp các thông tin về các điểm, vectơ, hoặc các mối quan hệ giữa chúng. Dựa vào đó, chúng ta sẽ xây dựng một phương án giải phù hợp.
(Nội dung lời giải chi tiết bài 4.13 trang 59 sẽ được trình bày tại đây, bao gồm các bước giải, các công thức sử dụng, và các giải thích rõ ràng. Ví dụ:)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. SA vuông góc với mặt phẳng (ABCD) và SA = a. Tính góc giữa đường thẳng SB và mặt phẳng (ABCD).
Ngoài bài 4.13 trang 59, sách bài tập Toán 11 Kết nối tri thức còn có nhiều bài tập tương tự liên quan đến vectơ trong không gian. Các bài tập này thường yêu cầu chúng ta:
Để giải các bài tập về vectơ một cách hiệu quả, bạn có thể tham khảo một số mẹo sau:
Để học tốt môn Toán 11, bạn có thể tham khảo thêm các tài liệu sau:
Bài 4.13 trang 59 sách bài tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp bạn củng cố kiến thức về vectơ trong không gian. Hy vọng với lời giải chi tiết và các mẹo giải bài tập mà giaitoan.edu.vn đã cung cấp, các em học sinh sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong môn Toán.