Bài 4.17 trang 59 sách bài tập Toán 11 Kết nối tri thức là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ và ứng dụng của vectơ trong hình học để giải quyết các bài toán cụ thể.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4.17 trang 59, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng.
Đề bài
Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng. Gọi G, H lần lượt là giao điểm của hai đường chéo của hai hình bình hành đó. Chứng minh rằng ba đường thẳng GH, CE, DF đôi một song song.
Phương pháp giải - Xem chi tiết
Dựa vào tính chất hình bình hành và tính chất đường trung bình của tam giác chứng minh 3 đường thẳng song song
Lời giải chi tiết
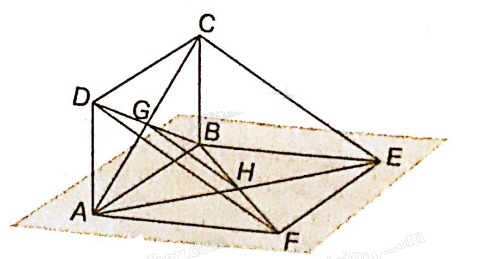
G là giao điểm hai đường chéo BD, AC của hình bình hành ABCD nên G là trung điểm của BD và AC.
H là giao điểm hai đường chéo BF, AE của hình bình hành ABEF nên H là trung điểm của BF và AE.
Xét tam giác BDF, GH là đường trung bình của tam giác nên GH song song với DF.
GH là đường trung bình tam giác ACE nên GH song song với CE.
Vậy ba đường thẳng GH, CE, DF đôi một song song.
Bài 4.17 trang 59 sách bài tập Toán 11 Kết nối tri thức yêu cầu chúng ta giải quyết một bài toán liên quan đến vectơ trong không gian. Để giải bài toán này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về vectơ, bao gồm:
Nội dung bài toán 4.17: (Nội dung bài toán cụ thể sẽ được chèn vào đây. Ví dụ: Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a, SA vuông góc với mặt phẳng (ABCD) và SA = a. Tính góc giữa đường thẳng SC và mặt phẳng (ABCD).)
Lời giải:
Ví dụ minh họa (giả sử bài toán là tính góc giữa SC và mặt phẳng (ABCD)):
Chọn hệ tọa độ Oxyz với gốc O là trung điểm của AC, trục Ox đi qua B, trục Oy đi qua D, trục Oz đi qua S. Khi đó, ta có:
Suy ra:
Gọi α là góc giữa SC và mặt phẳng (ABCD). Ta có:
sin(α) = |SC.n(ABCD)| / |SC| |n(ABCD)| = |-a| / (√(a2/4 + a2/4 + a2)) * 1 = a / (a√3/2) = 2/√3
Vậy α = arcsin(2/√3)
Lưu ý:
Các bài tập tương tự:
Hy vọng với lời giải chi tiết này, các em học sinh sẽ hiểu rõ hơn về cách giải bài 4.17 trang 59 sách bài tập Toán 11 Kết nối tri thức. Chúc các em học tập tốt!
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.