Bài 7.56 trang 43 sách bài tập Toán 11 - Kết nối tri thức với cuộc sống là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải bài tập.
Một bể chứa nước hình hộp chữ nhật \(ABCD \cdot A'B'C'D'\) được đặt trên một mái nhà nghiêng
Đề bài
Một bể chứa nước hình hộp chữ nhật \(ABCD \cdot A'B'C'D'\) được đặt trên một mái nhà nghiêng so với mặt đất nằm ngang góc \({10^ \circ },AB = 1{\rm{\;m}},AD = 1,5{\rm{\;m}}\), \(AA' = 1{\rm{\;m}}\). Đáy bể là hình chữ nhật \(ABCD\). Các điểm \(A,B\) cùng ở độ cao \(5{\rm{\;m}}\) (so với mặt đất), các điểm \(C,D\) ở độ cao lớn hơn so với độ cao của các điểm \(A,B\). Khi nước trong bể phẳng lặng người ta đo được khoảng cách giữa đường mép nước ở mặt phẳng \(\left( {ABB'A'} \right)\) và mặt đáy của bể là \(80{\rm{\;cm}}\). Tính thế tích của phần nước trong bể.
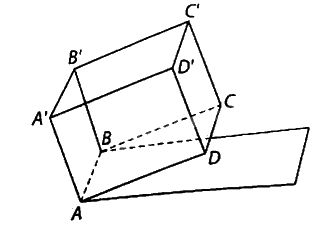
Phương pháp giải - Xem chi tiết
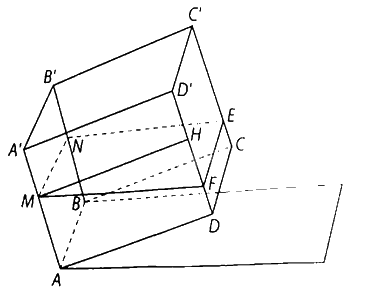
Gọi \(MN\) là đường mép nước ở trên mặt \(\left( {ABB'A'} \right),EF\) là đường mép nước trên mặt \(\left( {CDD'C'} \right)\).
Khi đó \(ABNM.DCEF\) là một hình chóp cựt.
Kẻ \(MH\) vuông góc với \(DD'\) tại \(H\) thì \(HF = MH \cdot {\rm{tan}}{10^ \circ } = {\rm{tan}}{10^ \circ }\left( {\rm{m}} \right)\).
Suy ra \(DF = DH - HF = AM - HF = 0,8 - {\rm{tan}}{10^ \circ } \approx 0,62\left( {{\rm{\;m}}} \right)\).
Tính: \({S_1} = {S_{DCEF}};{S_2} = {S_{ABNM}}\).
Tính \(V = \frac{1}{3} \cdot \left( {{S_1} + {S_2} + \sqrt {{S_1}{S_2}} } \right) \cdot AD\)
Lời giải chi tiết
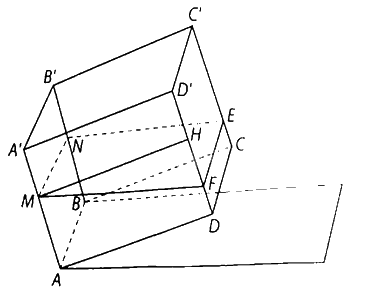
Gọi \(MN\) là đường mép nước ở trên mặt \(\left( {ABB'A'} \right),EF\) là đường mép nước trên mặt \(\left( {CDD'C'} \right)\).
Khi đó \(ABNM.DCEF\) là một hình chóp cựt.
Kẻ \(MH\) vuông góc với \(DD'\) tại \(H\) thì \(HF = MH \cdot {\rm{tan}}{10^ \circ } = {\rm{tan}}{10^ \circ }\left( {\rm{m}} \right)\).
Suy ra \(DF = DH - HF = AM - HF = 0,8 - {\rm{tan}}{10^ \circ } \approx 0,62\left( {{\rm{\;m}}} \right)\).
Ta có: \({S_1} = {S_{DCEF}} = DF \cdot CD \approx 0,62\left( {{\rm{\;}}{{\rm{m}}^2}} \right);{S_2} = {S_{ABNM}} = AB \cdot AM = 0,8\left( {{\rm{\;}}{{\rm{m}}^2}} \right)\).
Vậy thể tích phần nước trong bể là
\(V = \frac{1}{3} \cdot \left( {{S_1} + {S_2} + \sqrt {{S_1}{S_2}} } \right) \cdot AD = \frac{1}{3} \cdot \left( {0,62 + 0,8 + \sqrt {0,62 \cdot 0,8} } \right) \approx 0,71\left( {{\rm{\;}}{{\rm{m}}^3}} \right).\)
Bài 7.56 trang 43 sách bài tập Toán 11 - Kết nối tri thức với cuộc sống là một bài toán ứng dụng thực tế, đòi hỏi học sinh phải hiểu rõ về đạo hàm và cách sử dụng đạo hàm để giải quyết các vấn đề liên quan đến tốc độ thay đổi của một đại lượng.
Trước khi đi vào giải bài, chúng ta cần phân tích kỹ đề bài để xác định rõ yêu cầu và các thông tin đã cho. Đề bài thường cung cấp một hàm số mô tả một quá trình nào đó, và yêu cầu chúng ta tìm một giá trị cụ thể của hàm số tại một thời điểm nhất định, hoặc tìm điều kiện để hàm số đạt giá trị lớn nhất hoặc nhỏ nhất.
Để giải bài 7.56 trang 43, chúng ta sẽ sử dụng các bước sau:
Đề bài: (Giả sử đề bài cụ thể ở đây, ví dụ: Một vật chuyển động theo phương trình s(t) = t3 - 3t2 + 5t + 2. Tính vận tốc của vật tại thời điểm t = 2.)
Giải:
Để hiểu rõ hơn về cách giải bài toán này, chúng ta hãy xem xét một ví dụ khác. (Ví dụ cụ thể về một bài toán tương tự và lời giải chi tiết).
Khi giải các bài toán về đạo hàm, cần chú ý các điểm sau:
Để rèn luyện kỹ năng giải bài toán về đạo hàm, bạn có thể thử giải các bài tập tương tự sau:
Bài 7.56 trang 43 sách bài tập Toán 11 - Kết nối tri thức với cuộc sống là một bài toán quan trọng giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm trong thực tế. Hy vọng rằng với hướng dẫn chi tiết này, bạn đã có thể hiểu rõ cách giải bài toán này và tự tin giải các bài toán tương tự.