Bài 7.37 trang 41 sách bài tập Toán 11 - Kết nối tri thức là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 7.37 trang 41, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho hình chóp có đáy \(ABCD\) là hình thoi tâm \(O\), biết \(SO \bot \left( {ABCD} \right)\)
Đề bài
Cho hình chóp có đáy \(ABCD\) là hình thoi tâm \(O\), biết \(SO \bot \left( {ABCD} \right)\), \(AC = 2a\sqrt 3 ,BD = 2a\) và khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( {SBC} \right)\) bằng \(\frac{{a\sqrt 3 }}{2}\). Tính theo \(a\) thể tích khối chóp \(S.ABCD\).
Phương pháp giải - Xem chi tiết
Áp dụng công thức tính thể tích khối chóp: \({\rm{S}} = \frac{1}{3}{\rm{Bh}}\).
Trong đó: \({\rm{B}}\) là diện tích đa giác đáy
h là đường cao của hình chóp
Bước 1: Tính chiều cao \(SO\) của hình chóp
Phân tích: \(d\left( {A,\left( {SBC} \right)} \right) = 2 \cdot d\left( {O,\left( {SBC} \right)} \right) \Rightarrow d\left( {O,\left( {SBC} \right)} \right)\)
Dựng hình
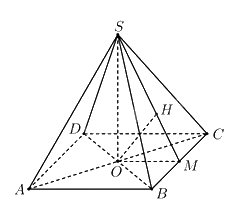
Khoảng cách từ \(d\left( {O,\left( {SBC} \right)} \right) = OH\)
Xét tam giác \(SOM\) vuông tại \(O\), đường cao \(OH\) nên \(\frac{1}{{O{H^2}}} = \frac{1}{{O{M^2}}} + \frac{1}{{O{S^2}}}\), suy ra \(SO\).
Bước 2: Tính diện tích đáy \(ABCD\)
Bước 3: Tính thể tích khối chóp \(S.ABCD\): \({V_{S \cdot ABCD}} = \frac{1}{3} \cdot {S_{ABCD}} \cdot SO\)
Lời giải chi tiết
Kẻ \(OM\) vuông góc với \(BC\) tại \(M,OH\) vuông góc với \(SM\) tại \(H\), ta chứng minh được \(OH \bot \left( {SBC} \right)\). Vì \(O\) là trung điểm của \(AC\) nên\(d\left( {A,\left( {SBC} \right)} \right) = 2 \cdot d\left( {O,\left( {SBC} \right)} \right) = 2 \cdot OH = \frac{{a\sqrt 3 }}{2}\),
suy ra \({\rm{OH}} = \frac{{{\rm{a}}\sqrt 3 }}{4}\).
Tam giác \(OBC\) vuông tại \(O\), có \(OB = a,OC = a\sqrt 3 \)
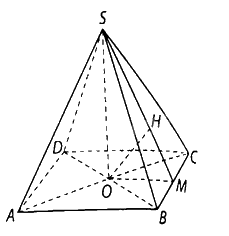
và đường cao \(OM\) nên \(OM = \frac{{OB \cdot OC}}{{BC}} = \frac{{a\sqrt 3 }}{2}\).
Tam giác \(SOM\) vuông tại \(O\), đường cao \(OH\) nên \(\frac{1}{{O{H^2}}} = \frac{1}{{O{M^2}}} + \frac{1}{{O{S^2}}}\), suy ra \(SO = \frac{a}{2}\).
Vậy \({V_{S \cdot ABCD}} = \frac{1}{3} \cdot {S_{ABCD}} \cdot SO = \frac{1}{3} \cdot \frac{1}{2} \cdot 2a\sqrt 3 \cdot 2a \cdot \frac{a}{2} = \frac{{{a^3}\sqrt 3 }}{3}\).
Bài 7.37 trang 41 sách bài tập Toán 11 - Kết nối tri thức thuộc chương trình học về đạo hàm của hàm số. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về:
Bài toán 7.37 thường yêu cầu học sinh thực hiện các thao tác sau:
Để giải bài 7.37 trang 41, ta thực hiện theo các bước sau:
Ví dụ, giả sử bài toán yêu cầu tìm cực trị của hàm số f(x) = x3 - 3x2 + 2.
Giải:
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| f'(x) | + | - | + | |
| f(x) | NB | ĐC | TB |
Vậy hàm số đạt cực đại tại x = 0, f(0) = 2 và đạt cực tiểu tại x = 2, f(2) = -2.
Để giải các bài tập về đạo hàm một cách hiệu quả, bạn nên:
Đạo hàm có rất nhiều ứng dụng trong thực tế, ví dụ như:
Hy vọng với lời giải chi tiết và hướng dẫn trên, các em học sinh sẽ hiểu rõ hơn về cách giải bài 7.37 trang 41 sách bài tập Toán 11 - Kết nối tri thức và tự tin hơn trong quá trình học tập.