Bài 1.4 trang 9 SGK Toán 7 tập 1 - Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng thực hiện các phép tính với số nguyên. Bài tập này yêu cầu học sinh vận dụng kiến thức về số nguyên âm, số nguyên dương và các quy tắc cộng, trừ số nguyên để tìm ra kết quả chính xác.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 1.4 trang 9 SGK Toán 7 tập 1 - Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
a) Trong các phân số sau, những phân số nào biểu diễn số hữu tỉ -0,625? b) Biểu diễn số hữu tỉ -0,625 trên trục số.
Đề bài
a) Trong các phân số sau, những phân số nào biểu diễn số hữu tỉ -0,625?
\(\frac{5}{{ - 8}};\frac{{10}}{{16}};\frac{{20}}{{ - 32}};\frac{{ - 10}}{{16}};\frac{{ - 25}}{{40}};\frac{{35}}{{ - 48}}.\)
b) Biểu diễn số hữu tỉ -0,625 trên trục số.
Phương pháp giải - Xem chi tiết
a) Bước 1: Viết -0,625 dưới dạng phân số
Bước 2: Rút gọn các phân số đã cho
Bước 3: Tìm các phân số bằng -0,625
b) Vẽ trục số
Lời giải chi tiết
a) Ta có: \( - 0,625 = \frac{{ - 625}}{{1000}}= \frac{{ - 625:125}}{{1000:125}} = \frac{{ - 5}}{8}\)
\(\begin{array}{l}\frac{5}{{ - 8}} = \frac{{ - 5}}{8};\\\frac{{10}}{{16}} = \frac{{10:2}}{{16:2}} = \frac{5}{8};\\\frac{{20}}{{ - 32}} = \frac{{20:( - 4)}}{{( - 32):( - 4)}} = \frac{{ - 5}}{8};\\\frac{{ - 10}}{{16}} = \frac{{( - 10):2}}{{16:2}} = \frac{{ - 5}}{8};\\\frac{{ - 25}}{{40}} = \frac{{( - 25):5}}{{40:5}} = \frac{{ - 5}}{8};\\\frac{{35}}{{ - 48}}\end{array}\)
Vậy các phân số biểu diễn số hữu tỉ -0,625 là:
\(\frac{5}{{ - 8}};\frac{{20}}{{ - 32}};\frac{{ - 10}}{{16}};\frac{{ - 25}}{{40}}\)
b) Ta có: \( - 0,625 = \frac{{ -5}}{{8}}\) nên ta biểu diễn số hữu tỉ \(\frac{{ -5}}{{8}}\) trên trục số.
Chia đoạn thẳng đơn vị thành 8 phần bằng nhau, lấy một đoạn làm đơn vị mới, đơn vị mới bằng \(\frac{1}{8}\) đơn vị cũ.
Lấy một điểm nằm trước O và cách O một đoạn bằng 5 đơn vị mới. Điểm đó biểu diễn số hữu tỉ \(\frac{{ -5}}{{8}}\)
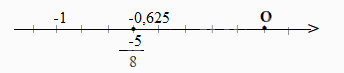
Bài 1.4 trang 9 SGK Toán 7 tập 1 - Kết nối tri thức yêu cầu chúng ta thực hiện các phép tính cộng, trừ số nguyên. Để giải bài tập này một cách chính xác, chúng ta cần nắm vững các quy tắc sau:
Bài tập 1.4 bao gồm một số câu hỏi yêu cầu tính toán các biểu thức chứa số nguyên. Ví dụ:
Dưới đây là lời giải chi tiết cho từng câu hỏi trong bài tập 1.4:
Đây là phép cộng hai số nguyên khác dấu. Ta lấy giá trị tuyệt đối của 3 là 3 và giá trị tuyệt đối của -5 là 5. Sau đó, ta lấy 5 trừ 3 và giữ nguyên dấu của số lớn (là -5). Vậy, 3 + (-5) = -2.
Đây cũng là phép cộng hai số nguyên khác dấu. Ta lấy giá trị tuyệt đối của -7 là 7 và giá trị tuyệt đối của 2 là 2. Sau đó, ta lấy 7 trừ 2 và giữ nguyên dấu của số lớn (là -7). Vậy, (-7) + 2 = -5.
Đây là phép cộng hai số nguyên cùng dấu. Ta cộng các giá trị tuyệt đối của chúng: 4 + 6 = 10. Sau đó, ta giữ nguyên dấu âm. Vậy, (-4) + (-6) = -10.
Để trừ hai số nguyên, ta cộng số bị trừ (8) với số đối của số trừ (-10). Vậy, 8 - 10 = 8 + (-10). Đây là phép cộng hai số nguyên khác dấu. Ta lấy giá trị tuyệt đối của 8 là 8 và giá trị tuyệt đối của -10 là 10. Sau đó, ta lấy 10 trừ 8 và giữ nguyên dấu của số lớn (là -10). Vậy, 8 - 10 = -2.
Để nắm vững hơn về các phép tính với số nguyên, các em có thể tham khảo thêm các bài tập tương tự trong SGK Toán 7 tập 1 - Kết nối tri thức và các tài liệu luyện tập khác. Ngoài ra, các em cũng có thể tìm hiểu thêm về các ứng dụng của số nguyên trong thực tế, ví dụ như trong việc biểu diễn nhiệt độ, độ cao, hoặc các khoản nợ.
Bài 1.4 trang 9 SGK Toán 7 tập 1 - Kết nối tri thức là một bài tập cơ bản nhưng quan trọng trong chương trình học Toán 7. Việc nắm vững các quy tắc cộng, trừ số nguyên và áp dụng chúng một cách linh hoạt sẽ giúp các em giải quyết các bài tập tương tự một cách dễ dàng và hiệu quả. Chúc các em học tốt!