Bài học về Tam giác cân và Đường trung trực của đoạn thẳng là một phần quan trọng trong chương trình Toán 7 Kết nối tri thức.
Nắm vững kiến thức này sẽ giúp các em giải quyết các bài toán hình học một cách dễ dàng và hiệu quả.
Giaitoan.edu.vn cung cấp lý thuyết chi tiết, bài tập minh họa và hướng dẫn giải bài tập SGK Toán 7 Kết nối tri thức một cách dễ hiểu nhất.
1. Tam giác cân và tính chất
1. Tam giác cân và tính chất
* Định nghĩa:
Tam giác cân là tam giác có hai cạnh bằng nhau.
2 cạnh bằng nhau được gọi là 2 cạnh bên. Cạnh còn lại là cạnh đáy.
Ví dụ:
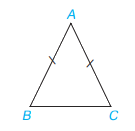
Tam giác ABC là tam giác cân tại A, có:
- Cạnh bên : AB, AC
- Cạnh đáy: BC
- Góc ở đỉnh: Góc A
- Góc ở đáy: góc B và góc C
* Tính chất của tam giác cân:
Trong một tam giác cân, 2 góc ở đáy bằng nhau.
Ngược lại, nếu một tam giác có 2 góc bằng nhau thì tam giác đó cân.
* Tam giác đều:
Tam giác đều là tam giác có 3 cạnh bằng nhau.
Tính chất: Tam giác đều có 3 góc bằng nhau, đều bằng 60 độ.
2. Đường trung trực của một đoạn thẳng
Đường thẳng vuông góc với 1 đoạn thẳng tại trung điểm của nó là đường trung trực của đoạn thẳng đó.
Đường trung trực của 1 đoạn thẳng cũng là trục đối xứng của đoạn thẳng đó.
* Tính chất đường trung trực
Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều 2 mút của đoạn thẳng đó.
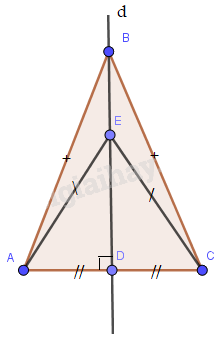
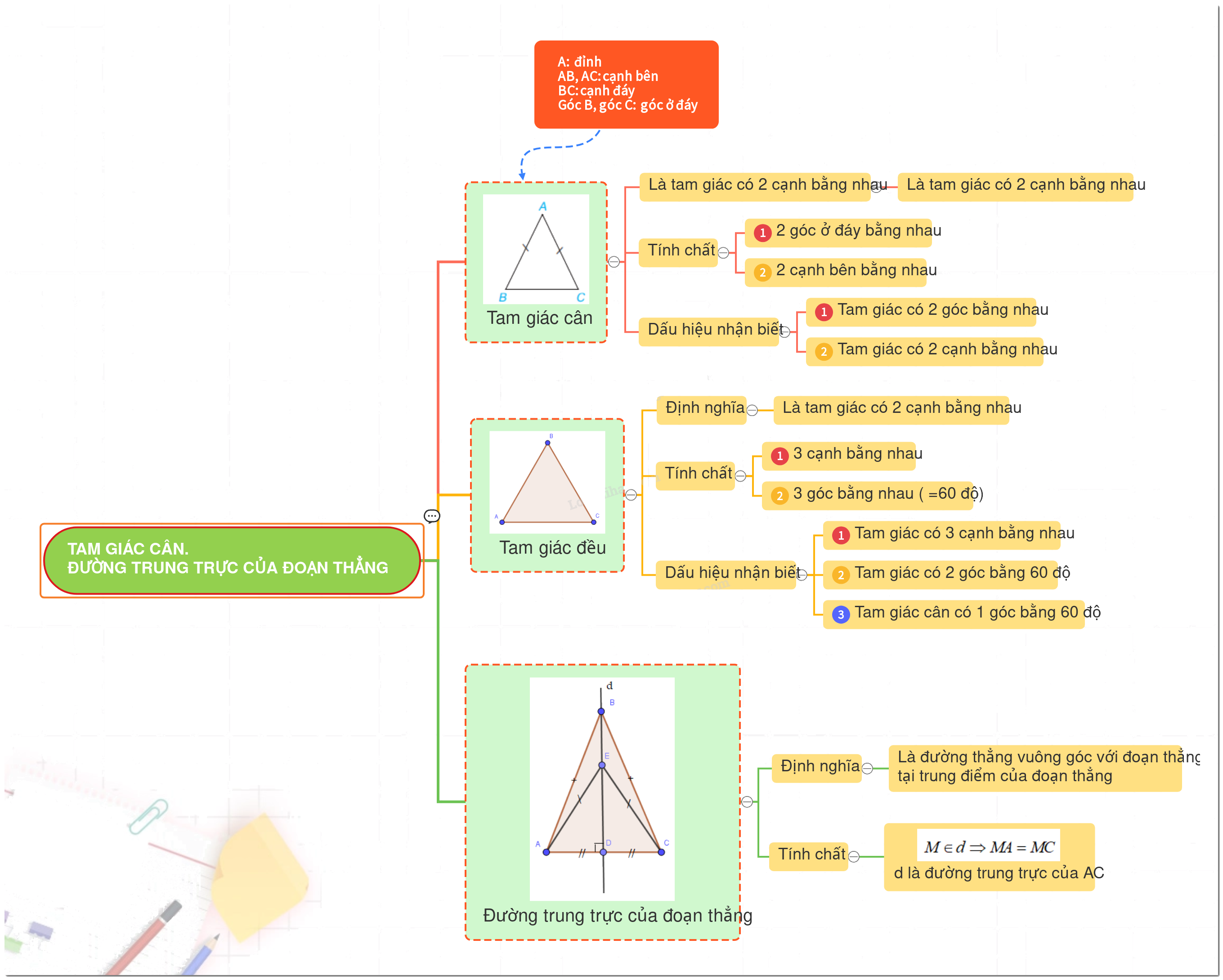
Trong chương trình Toán 7, kiến thức về tam giác cân và đường trung trực của đoạn thẳng đóng vai trò quan trọng trong việc xây dựng nền tảng hình học vững chắc. Bài viết này sẽ cung cấp một cách chi tiết và dễ hiểu về lý thuyết này, dựa trên sách giáo khoa Toán 7 Kết nối tri thức.
Định nghĩa: Tam giác cân là tam giác có hai cạnh bằng nhau.
Tính chất:
Ví dụ: Tam giác ABC cân tại A, thì AB = AC và ∠B = ∠C.
Định nghĩa: Đường trung trực của một đoạn thẳng là đường thẳng vuông góc với đoạn thẳng đó tại trung điểm của nó.
Tính chất:
Ví dụ: Gọi M là trung điểm của đoạn thẳng AB. Đường thẳng d vuông góc với AB tại M là đường trung trực của đoạn thẳng AB.
Trong một tam giác cân, đường trung tuyến kẻ từ đỉnh góc nhọn xuống cạnh đáy đồng thời là đường trung trực của cạnh đáy.
Điều này có nghĩa là, nếu một tam giác có một đường trung tuyến đồng thời là đường trung trực của cạnh đáy, thì tam giác đó là tam giác cân.
Bài tập 1: Cho tam giác ABC cân tại A. Biết ∠A = 80°. Tính số đo ∠B và ∠C.
Giải: Vì tam giác ABC cân tại A nên ∠B = ∠C.
Ta có ∠A + ∠B + ∠C = 180°
=> 80° + ∠B + ∠B = 180°
=> 2∠B = 100°
=> ∠B = ∠C = 50°
Bài tập 2: Cho đoạn thẳng AB và điểm M nằm ngoài đoạn thẳng đó. Vẽ đường trung trực d của đoạn thẳng AB. Chứng minh rằng nếu MA = MB thì M nằm trên đường trung trực d.
Giải: Theo tính chất của đường trung trực, mọi điểm cách đều hai mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.
Vì MA = MB nên M nằm trên đường trung trực d của đoạn thẳng AB.
Lý thuyết về tam giác cân và đường trung trực có nhiều ứng dụng trong thực tế và trong các bài toán hình học khác. Ví dụ:
Để nắm vững kiến thức về tam giác cân và đường trung trực, các em nên luyện tập thường xuyên các bài tập trong sách giáo khoa và các bài tập nâng cao. Ngoài ra, các em có thể tham khảo các tài liệu học tập trực tuyến và các video hướng dẫn trên giaitoan.edu.vn.
Hy vọng bài viết này đã cung cấp cho các em những kiến thức cơ bản và hữu ích về lý thuyết Tam giác cân và Đường trung trực của đoạn thẳng SGK Toán 7 Kết nối tri thức. Chúc các em học tập tốt!