Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 7 tại giaitoan.edu.vn. Chúng tôi xin giới thiệu lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 41, 42, 43 sách giáo khoa Toán 7 tập 1 - Kết nối tri thức.
Với đội ngũ giáo viên giàu kinh nghiệm, chúng tôi cam kết cung cấp cho các em những phương pháp giải bài tập hiệu quả nhất, giúp các em nắm vững kiến thức và tự tin hơn trong học tập.
Quan sát hình vẽ bên. Em hãy nhận xét về mối quan hệ về đỉnh, về cạnh của hai góc được đánh dấu...Cho ba tia Ox, Oy, Oz như Hình 3.1, trong đó Ox và Oy là hai tia đối nhau. a) Em hãy nhận xét về quan hệ về đỉnh, về cạnh của hai góc xOz và zOy. b) Đo rồi tính tổng số đo góc hai góc xOz và zOy.
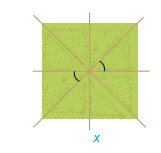
Quan sát hình ảnh hai góc được đánh dấu trong hình bên. Em hãy nhận xét quan hệ về đỉnh, về cạnh của hia góc được đánh dấu.
Phương pháp giải:
Xác định đỉnh, cạnh của hai góc được đánh dấu rồi nhận xét.
Lời giải chi tiết:
2 góc trên hình có cùng đỉnh; từng cạnh của góc này là tia đối của cạnh của góc kia.
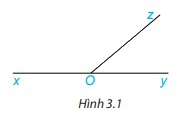
Cho ba tia Ox, Oy, Oz như Hình 3.1, trong đó Ox và Oy là hai tia đối nhau.
a) Em hãy nhận xét về quan hệ về đỉnh, về cạnh của hai góc xOz và zOy.
b) Đo rồi tính tổng số đo góc hai góc xOz và zOy.
Phương pháp giải:
a) Xác định đỉnh, cạnh của hai góc được đánh dấu rồi nhận xét.
b) Đo góc: đặt đỉnh của góc trùng với gốc của thước, 1 cạnh của góc trùng với vạch 0, cạnh còn lại của góc trùng với vạch nào thì đó là số đo góc.
Lời giải chi tiết:
a) Đỉnh của góc xOz và zOy cùng là đỉnh O
2 góc xOz và zOy có chung cạnh Oz, cạnh còn lại (Ox và Oy) là 2 tia đối nhau.
b) \(\widehat{xOz}=140^0, \widehat{zOy}=40^0\)
Ta được: \(\widehat{xOz}+\widehat{zOy}=140^0+40^0=180^0\)
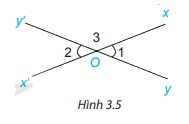
Cho hai đường thẳng xx’ và yy’ cắt nhau tại O (H.3.5)
a) Dự đoán xem hai góc xOy và x’Oy’ có bằng nhau không?
b) Đo rồi so sánh số đo hai góc xOy và x’Oy’
Phương pháp giải:
Đo 2 góc rồi so sánh
Lời giải chi tiết:
a) Em dự đoán xem hai góc xOy và x’Oy’ có bằng nhau.
b) \(\widehat{xOy} = \widehat{x’Oy’} = 31^0\)
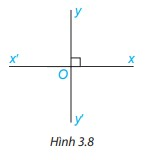
Hai đường thẳng xx’ và yy’ cắt nhau tại O sao cho góc xOy vuông (H.3.8). Khi đó các góc yOx’, x’Oy’, xOy’ cũng đều là góc vuông. Vì sao?
Phương pháp giải:
Sử dụng tính chất: 2 góc kề bù có tổng là 180 độ, 2 góc đối đỉnh bằng nhau.
Lời giải chi tiết:
Góc x’Oy’ và xOy là hai góc đối đỉnh nên \(\widehat {x'Oy'} = \widehat {xOy} = 90^\circ \)
Góc xOy’ và xOy là hai góc kề bù nên
\(\begin{array}{l}\widehat {xOy'} + \widehat {xOy} = 180^\circ \\ \Rightarrow \widehat {xOy'} + 90^\circ = 180^\circ \\ \Rightarrow \widehat {xOy'} = 180^\circ - 90^\circ = 90^\circ \end{array}\)
Góc x’Oy và xOy là hai góc kề bù nên
\(\begin{array}{l}\widehat {x'Oy} + \widehat {xOy} = 180^\circ \\ \Rightarrow \widehat {x'Oy} + 90^\circ = 180^\circ \\ \Rightarrow \widehat {x'Oy} = 180^\circ - 90^\circ = 90^\circ \end{array}\)
Hai góc được đánh dấu trong hình nào dưới đây là hai góc đối đỉnh?
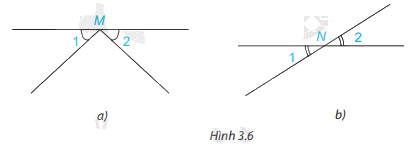
Phương pháp giải:
Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đốicủa một cạnh của góc kia.
Lời giải chi tiết:
2 góc ở hình 3.6.b là hai góc đối đỉnh vì 2 góc này có mỗi cạnh của góc này là tia đốicủa một cạnh của góc kia.
Hai góc được đánh dấu trong hình nào dưới đây là hai góc kề bù?
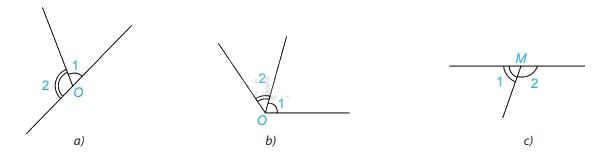
Phương pháp giải:
2 góc có một cạnh chung, hai cạnh còn lại là hai tia đối nhau được gọi là 2 góc kề bù
Lời giải chi tiết:
Xét hình a: \(\widehat {{O_1}}\) và \( \widehat {{O_2}}\) là hai góc kề bù vì 2 góc này có một cạnh chung, hai cạnh còn lại là hai tia đối nhau
Xét hình b: \(\widehat {{O_1}} \) và \( \widehat {{O_2}}\) không là hai góc kề bù vì 2 góc này có một cạnh chung nhưng hai cạnh còn lại không là hai tia đối nhau
Xét hình c: \(\widehat {{M_1}} \) và \( \widehat {{M_2}}\) là hai góc kề bù vì 2 góc này có một cạnh chung, hai cạnh còn lại là hai tia đối nhau.
Quan sát hình vẽ bên. Em hãy nhận xét về mối quan hệ về đỉnh, về cạnh của hai góc được đánh dấu.
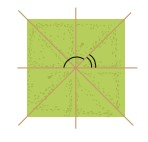
Phương pháp giải:
Xác định đỉnh, cạnh của hai góc được đánh dấu rồi nhận xét.
Lời giải chi tiết:
2 góc được đánh dấu là 2 góc có: chung đỉnh; có chung một cạnh, cạnh còn lại là 2 tia đối nhau
Viết tên hai góc kề bù trong Hình 3.4 và tính số đo góc mOt
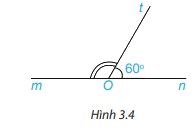
Phương pháp giải:
2 góc có một cạnh chung, hai cạnh còn lại là hai tia đối nhau được gọi là 2 góc kề bù.
Tổng số đo của 2 góc kề bù là 180 độ.
Lời giải chi tiết:
2 góc kề bù trong hình là: góc mOt và tOn
Ta có:
\(\begin{array}{l}\widehat {mOt} + \widehat {tOn} = 180^\circ \\\widehat {mOt} = 180^\circ - \widehat {tOn} = 180^\circ - 60^\circ = 120^\circ \end{array}\)
Quan sát hình vẽ bên. Em hãy nhận xét về mối quan hệ về đỉnh, về cạnh của hai góc được đánh dấu.
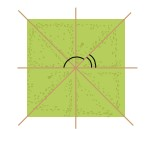
Phương pháp giải:
Xác định đỉnh, cạnh của hai góc được đánh dấu rồi nhận xét.
Lời giải chi tiết:
2 góc được đánh dấu là 2 góc có: chung đỉnh; có chung một cạnh, cạnh còn lại là 2 tia đối nhau
Cho ba tia Ox, Oy, Oz như Hình 3.1, trong đó Ox và Oy là hai tia đối nhau.
a) Em hãy nhận xét về quan hệ về đỉnh, về cạnh của hai góc xOz và zOy.
b) Đo rồi tính tổng số đo góc hai góc xOz và zOy.
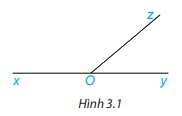
Phương pháp giải:
a) Xác định đỉnh, cạnh của hai góc được đánh dấu rồi nhận xét.
b) Đo góc: đặt đỉnh của góc trùng với gốc của thước, 1 cạnh của góc trùng với vạch 0, cạnh còn lại của góc trùng với vạch nào thì đó là số đo góc.
Lời giải chi tiết:
a) Đỉnh của góc xOz và zOy cùng là đỉnh O
2 góc xOz và zOy có chung cạnh Oz, cạnh còn lại (Ox và Oy) là 2 tia đối nhau.
b) \(\widehat{xOz}=140^0, \widehat{zOy}=40^0\)
Ta được: \(\widehat{xOz}+\widehat{zOy}=140^0+40^0=180^0\)
Hai góc được đánh dấu trong hình nào dưới đây là hai góc kề bù?
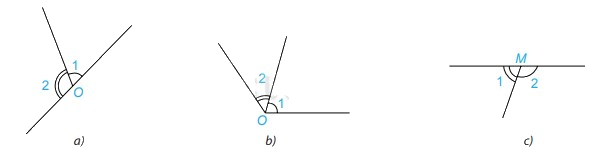
Phương pháp giải:
2 góc có một cạnh chung, hai cạnh còn lại là hai tia đối nhau được gọi là 2 góc kề bù
Lời giải chi tiết:
Xét hình a: \(\widehat {{O_1}}\) và \( \widehat {{O_2}}\) là hai góc kề bù vì 2 góc này có một cạnh chung, hai cạnh còn lại là hai tia đối nhau
Xét hình b: \(\widehat {{O_1}} \) và \( \widehat {{O_2}}\) không là hai góc kề bù vì 2 góc này có một cạnh chung nhưng hai cạnh còn lại không là hai tia đối nhau
Xét hình c: \(\widehat {{M_1}} \) và \( \widehat {{M_2}}\) là hai góc kề bù vì 2 góc này có một cạnh chung, hai cạnh còn lại là hai tia đối nhau.
Viết tên hai góc kề bù trong Hình 3.4 và tính số đo góc mOt
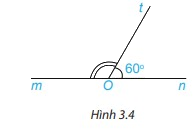
Phương pháp giải:
2 góc có một cạnh chung, hai cạnh còn lại là hai tia đối nhau được gọi là 2 góc kề bù.
Tổng số đo của 2 góc kề bù là 180 độ.
Lời giải chi tiết:
2 góc kề bù trong hình là: góc mOt và tOn
Ta có:
\(\begin{array}{l}\widehat {mOt} + \widehat {tOn} = 180^\circ \\\widehat {mOt} = 180^\circ - \widehat {tOn} = 180^\circ - 60^\circ = 120^\circ \end{array}\)
Quan sát hình ảnh hai góc được đánh dấu trong hình bên. Em hãy nhận xét quan hệ về đỉnh, về cạnh của hia góc được đánh dấu.
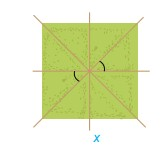
Phương pháp giải:
Xác định đỉnh, cạnh của hai góc được đánh dấu rồi nhận xét.
Lời giải chi tiết:
2 góc trên hình có cùng đỉnh; từng cạnh của góc này là tia đối của cạnh của góc kia.
Cho hai đường thẳng xx’ và yy’ cắt nhau tại O (H.3.5)
a) Dự đoán xem hai góc xOy và x’Oy’ có bằng nhau không?
b) Đo rồi so sánh số đo hai góc xOy và x’Oy’
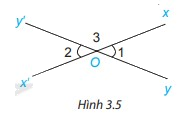
Phương pháp giải:
Đo 2 góc rồi so sánh
Lời giải chi tiết:
a) Em dự đoán xem hai góc xOy và x’Oy’ có bằng nhau.
b) \(\widehat{xOy} = \widehat{x’Oy’} = 31^0\)
Hai góc được đánh dấu trong hình nào dưới đây là hai góc đối đỉnh?
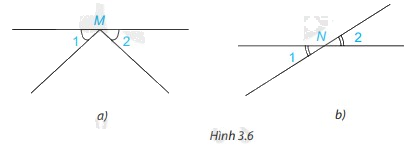
Phương pháp giải:
Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đốicủa một cạnh của góc kia.
Lời giải chi tiết:
2 góc ở hình 3.6.b là hai góc đối đỉnh vì 2 góc này có mỗi cạnh của góc này là tia đốicủa một cạnh của góc kia.
Hai đường thẳng xx’ và yy’ cắt nhau tại O sao cho góc xOy vuông (H.3.8). Khi đó các góc yOx’, x’Oy’, xOy’ cũng đều là góc vuông. Vì sao?
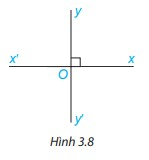
Phương pháp giải:
Sử dụng tính chất: 2 góc kề bù có tổng là 180 độ, 2 góc đối đỉnh bằng nhau.
Lời giải chi tiết:
Góc x’Oy’ và xOy là hai góc đối đỉnh nên \(\widehat {x'Oy'} = \widehat {xOy} = 90^\circ \)
Góc xOy’ và xOy là hai góc kề bù nên
\(\begin{array}{l}\widehat {xOy'} + \widehat {xOy} = 180^\circ \\ \Rightarrow \widehat {xOy'} + 90^\circ = 180^\circ \\ \Rightarrow \widehat {xOy'} = 180^\circ - 90^\circ = 90^\circ \end{array}\)
Góc x’Oy và xOy là hai góc kề bù nên
\(\begin{array}{l}\widehat {x'Oy} + \widehat {xOy} = 180^\circ \\ \Rightarrow \widehat {x'Oy} + 90^\circ = 180^\circ \\ \Rightarrow \widehat {x'Oy} = 180^\circ - 90^\circ = 90^\circ \end{array}\)
Mục 1 của chương trình Toán 7 tập 1 - Kết nối tri thức tập trung vào việc ôn tập và mở rộng kiến thức về các phép toán cơ bản trên số tự nhiên, số nguyên, phân số. Các bài tập trong trang 41, 42, 43 SGK Toán 7 tập 1 yêu cầu học sinh vận dụng các kiến thức này để giải quyết các bài toán thực tế, rèn luyện kỹ năng tính toán và tư duy logic.
Bài 1 yêu cầu học sinh thực hiện các phép tính cộng, trừ, nhân, chia các số tự nhiên, số nguyên, phân số. Để giải bài tập này, học sinh cần nắm vững thứ tự thực hiện các phép toán và quy tắc dấu ngoặc.
Bài 2 yêu cầu học sinh tìm giá trị của x thỏa mãn các phương trình đơn giản. Để giải bài tập này, học sinh cần sử dụng các phép biến đổi tương đương để đưa phương trình về dạng x = ...
Bài 3 thường là các bài toán ứng dụng các kiến thức đã học vào các tình huống thực tế. Để giải bài tập này, học sinh cần đọc kỹ đề bài, xác định các yếu tố quan trọng và lập luận logic để tìm ra lời giải.
Ví dụ: Một cửa hàng có 25 kg gạo. Sau khi bán đi 1/5 số gạo, cửa hàng còn lại bao nhiêu kg gạo? Giải: Số gạo đã bán là 25 x 1/5 = 5 kg. Số gạo còn lại là 25 - 5 = 20 kg.
Khi giải bài tập Toán 7, học sinh cần chú ý đến các quy tắc dấu ngoặc, thứ tự thực hiện các phép toán và quy tắc chuyển vế. Ngoài ra, học sinh cũng cần rèn luyện kỹ năng tính toán nhanh và chính xác.
Hy vọng với lời giải chi tiết và phương pháp giải bài tập hiệu quả mà giaitoan.edu.vn cung cấp, các em học sinh sẽ tự tin hơn trong việc học tập môn Toán 7. Chúc các em học tốt!
| Bài tập | Nội dung |
|---|---|
| Bài 1 | Tính các biểu thức |
| Bài 2 | Tìm x |
| Bài 3 | Bài toán thực tế |