Chào mừng các em học sinh lớp 7 đến với bài học về Lý thuyết Làm quen với số thập phân vô hạn tuần hoàn trong chương trình Toán 7 - Kết nối tri thức. Bài học này sẽ giúp các em hiểu rõ khái niệm về số thập phân vô hạn tuần hoàn, cách nhận biết và biểu diễn chúng.
Tại giaitoan.edu.vn, chúng tôi cung cấp tài liệu học tập đầy đủ, bài giảng chi tiết và bài tập thực hành đa dạng để hỗ trợ các em học tập hiệu quả nhất.
1. Số thập phân vô hạn tuần hoàn
1. Số thập phân vô hạn tuần hoàn
Ví dụ: Các số thập phân đã học như -4,3 ; 0,35;… còn được gọi là số thập phân hữu hạn.
Các số -0,2(7) ; 1,3(18) ; 5,(1) ;…. là những số thập phân vô hạn tuần hoàn với chu kì lần lượt là 7 ; 18 ; 1.
+ Mỗi số thập phân vô hạn tuần hoàn biểu diễn 1 số hữu tỉ
Chú ý:
+ Mọi số hữu tỉ đều viết được dưới dạng số thập phân hữu hạn hoặc vô hạn tuần hoàn.
+ Nếu phân số tối giản với mẫu dương mà mẫu không có ước nguyên tố nào khác 2 và 5 thì phân số đó viết được dưới dạng số thập phân hữu hạn.
Ví dụ: \(\frac{3}{{80}} = \frac{3}{{{2^4}.5}} = \frac{{{{3.5}^3}}}{{{2^4}{{.5.5}^3}}} = \frac{{375}}{{10000}} = 0,0375\)
+ Nếu phân số tối giản với mẫu dương mà mẫu có ước nguyên tố khác 2 và 5 thì phân số đó viết được dưới dạng số thập phân vô hạn tuần hoàn.
Ví dụ: \(\frac{7}{{30}} = 0,2333.... = 0,2(3)\)
2. Làm tròn số thập phân căn cứ vào độ chính xác cho trước
Khi làm tròn đến môt hàng nào đó, kết quả làm tròn có độ chính xác bằng một nửa đơn vị hàng làm tròn.
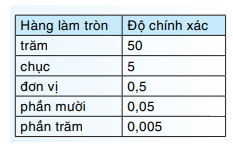
Ví dụ: Làm tròn số 2,13452….với độ chính xác 0,005, tức là làm tròn số 2,13452…. đến hàng phân trăm, ta được 2,13.
Trong chương trình Toán 7, việc làm quen với số thập phân vô hạn tuần hoàn là một bước quan trọng để xây dựng nền tảng vững chắc cho các kiến thức toán học nâng cao hơn. Bài viết này sẽ cung cấp một cái nhìn tổng quan và chi tiết về lý thuyết này, giúp học sinh hiểu rõ khái niệm, cách nhận biết và các tính chất cơ bản của số thập phân vô hạn tuần hoàn.
Số thập phân vô hạn tuần hoàn là số thập phân mà phần thập phân có một chuỗi các chữ số lặp đi lặp lại vô hạn. Chuỗi lặp lại này được gọi là chu kỳ của số thập phân vô hạn tuần hoàn. Ví dụ: 0,333..., 1,2(3), 5,123(45).
Để nhận biết một số thập phân vô hạn tuần hoàn, ta cần quan sát phần thập phân của số đó. Nếu phần thập phân có một chuỗi các chữ số lặp đi lặp lại vô hạn, thì đó là một số thập phân vô hạn tuần hoàn.
Có hai cách chính để biểu diễn số thập phân vô hạn tuần hoàn:
Việc chuyển đổi số thập phân vô hạn tuần hoàn thành phân số là một kỹ năng quan trọng. Dưới đây là các bước thực hiện:
Ví dụ: Chuyển đổi 0,3 thành phân số:
Số thập phân vô hạn tuần hoàn có một số tính chất quan trọng:
Để củng cố kiến thức về số thập phân vô hạn tuần hoàn, các em có thể thực hành các bài tập sau:
Hi vọng rằng bài viết này đã cung cấp cho các em một cái nhìn toàn diện về lý thuyết Làm quen với số thập phân vô hạn tuần hoàn trong chương trình Toán 7 - Kết nối tri thức. Việc nắm vững kiến thức này sẽ giúp các em tự tin hơn trong việc giải quyết các bài toán liên quan đến số thập phân và chuẩn bị tốt cho các bài học tiếp theo.