Bài 4.39 trang 87 SGK Toán 7 tập 1 thuộc chương trình Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng áp dụng các kiến thức đã học về tam giác cân vào giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4.39 này, giúp các em học sinh nắm vững phương pháp giải và tự tin hơn trong các bài kiểm tra.
Cho tam giác ABC vuông tại A có B = 60°. Trên cạnh BC lấy điểm M sao cho CAM=30. Chứng minh rằng: a) Tam giác CAM cân tại M; b) Tam giác BAM là tam giác đều; c) M là trung điểm của đoạn thẳng BC.
Đề bài
Cho tam giác ABC vuông tại A có B = 60°. Trên cạnh BC lấy điểm M sao cho \(\widehat {CAM} = {30^o}\). Chứng minh rằng:
a) Tam giác CAM cân tại M;
b) Tam giác BAM là tam giác đều;
c) M là trung điểm của đoạn thẳng BC.
Phương pháp giải - Xem chi tiết
a) Dùng tính chất tổng 3 góc trong 1 tam giác bằng 180 độ suy ra góc A bằng góc C.
b) Chứng minh tam giác ABM cân có 1 góc bằng 60 độ
c) Dùng tính chất tổng 3 góc trong 1 tam giác bằng 180 độ để tính số đo 3 góc từ đó suy ra tam giác đều
Lời giải chi tiết
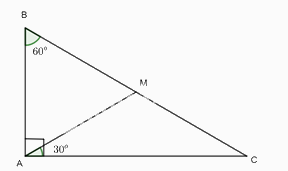
a) Xét tam giác ABC có:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = {180^o}\\ {90^o} + {60^o} + \widehat C = {180^o}\\ \widehat C = {30^o}\end{array}\)
Xét tam giác CAM có \(\widehat A = \widehat C = {30^o}\)
Suy ra tam giác CAM cân tại M.
b) Xét tam giác CAM có:
\(\begin{array}{l}\widehat C + \widehat {CMA} + \widehat {CAM} = {180^o}\\ {30^o} + \widehat {CMA} + {30^o} = {180^o}\\ \widehat {CMA} = {120^o}\\ \widehat {BMA} = {180^o} - \widehat {CMA} = {180^o} - {120^o} = {60^o}\end{array}\)
Xét tam giác ABM có:
\(\begin{array}{l}\widehat B + \widehat {BMA} + \widehat {BAM} = {180^o}\\ {60^o} + {60^o} + \widehat {BAM} = {180^o}\\ \widehat {BAM} = {60^o}\end{array}\)
Do \(\widehat {BAM} = \widehat {BMA} = \widehat {ABM} = {60^o}\) nên tam giác ABM đều.
c) Vì \(\Delta ABM\) đều nên \(AB = BM = AM\)
Mà \(\Delta CAM\) cân tại M nên MA = MC
Suy ra MB = MC. Mà M nằm giữa B và C
Do đó M là trung điểm của BC.
Bài 4.39 yêu cầu chúng ta xét hình vẽ và chứng minh một số tính chất liên quan đến tam giác cân. Để giải bài này, chúng ta cần nắm vững định nghĩa tam giác cân, các tính chất của tam giác cân (góc đối diện cạnh đáy bằng nhau, đường cao ứng với cạnh đáy đồng thời là đường trung tuyến và đường phân giác) và các dấu hiệu nhận biết tam giác cân.
Cho tam giác ABC cân tại A. Gọi D là trung điểm của BC. Chứng minh rằng:
a) Chứng minh AD là đường trung tuyến của tam giác ABC:
Theo đề bài, D là trung điểm của BC. Điều này có nghĩa là BD = DC. Theo định nghĩa đường trung tuyến của tam giác, đường trung tuyến là đoạn thẳng nối một đỉnh của tam giác với trung điểm của cạnh đối diện. Vì AD nối đỉnh A với trung điểm D của cạnh BC, nên AD là đường trung tuyến của tam giác ABC.
b) Chứng minh AD là đường cao của tam giác ABC:
Vì tam giác ABC cân tại A, nên AB = AC. Xét tam giác ABD và tam giác ACD, ta có:
Do đó, tam giác ABD = tam giác ACD (c-c-c). Suy ra ∠ADB = ∠ADC (hai góc tương ứng). Vì ∠ADB và ∠ADC là hai góc kề bù, nên ∠ADB + ∠ADC = 180°. Mà ∠ADB = ∠ADC, nên ∠ADB = ∠ADC = 90°. Vậy AD vuông góc với BC tại D, do đó AD là đường cao của tam giác ABC.
c) Chứng minh AD là đường phân giác của tam giác ABC:
Vì tam giác ABC cân tại A, nên ∠B = ∠C. Xét tam giác ABD và tam giác ACD, ta có:
Do đó, tam giác ABD = tam giác ACD (c-g-c). Suy ra ∠BAD = ∠CAD (hai góc tương ứng). Vậy AD là đường phân giác của tam giác ABC.
Qua bài giải trên, chúng ta đã chứng minh được rằng trong một tam giác cân, đường trung tuyến, đường cao và đường phân giác kẻ từ đỉnh góc cân xuống cạnh đáy là một. Đây là một tính chất quan trọng cần ghi nhớ khi giải các bài toán liên quan đến tam giác cân.
Để hiểu rõ hơn về tam giác cân và các tính chất của nó, các em có thể tham khảo thêm các bài tập tương tự trong SGK Toán 7 tập 1 - Kết nối tri thức. Ngoài ra, các em cũng có thể tìm kiếm các tài liệu học tập trực tuyến hoặc tham gia các khóa học toán online để nâng cao kiến thức và kỹ năng giải toán.
Giả sử AB = AC = 5cm, BC = 6cm. Tính độ dài AD.
Vì AD là đường cao của tam giác ABC, nên tam giác ADB là tam giác vuông tại D. Áp dụng định lý Pitago vào tam giác ADB, ta có:
AD2 + BD2 = AB2
AD2 + (BC/2)2 = AB2
AD2 + (6/2)2 = 52
AD2 + 32 = 25
AD2 + 9 = 25
AD2 = 16
AD = 4cm
Vậy độ dài AD là 4cm.
Khi giải các bài toán về tam giác cân, các em cần chú ý đến việc vận dụng linh hoạt các định nghĩa, tính chất và dấu hiệu nhận biết tam giác cân. Đồng thời, các em cũng cần rèn luyện kỹ năng vẽ hình chính xác và trình bày lời giải một cách logic, rõ ràng.