Bài 4.38 trang 87 SGK Toán 7 tập 1 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 7. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về các góc tạo bởi đường thẳng cắt đường thẳng để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4.38 trang 87 SGK Toán 7 tập 1 - Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Cho tam giác ABC cân tại A có A= 120 . Trên cạnh BC lấy hai điểm M, N sao cho MA, NA lần lượt vuông góc với AB, AC. Chứng minh rằng:
Đề bài
Cho tam giác ABC cân tại A có \(\widehat {A{\rm{ }}} = 120^\circ \). Trên cạnh BC lấy hai điểm M, N sao cho MA, NA lần lượt vuông góc với AB, AC. Chứng minh rằng:
a) \(\Delta \)BAM = \(\Delta \)CAN;
b) Các tam giác ANB, AMC lần lượt cân tại N, M.
Phương pháp giải - Xem chi tiết
a) Chứng minh 2 tam giác bằng nhau theo trường hợp g-c-g
b) Chứng minh tam giác có 2 cạnh bằng nhau hoặc 2 góc bằng nhau
Lời giải chi tiết
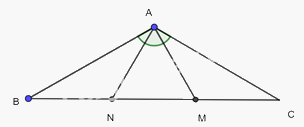
a) Xét 2 tam giác vuông BAM và CAN có:
\(\widehat{BAM} = \widehat{CAM}(=90^0)\)
AB=AC (Do tam giác ABC cân tại A)
\(\widehat B = \widehat C\) (Do tam giác ABC cân tại A)
=>\(\Delta BAM = \Delta CAN\)(g.c.g)
b) Cách 1:
Xét tam giác ABC cân tại A, có \(\widehat {A{\rm{ }}} = 120^\circ \) có:
\(\widehat B = \widehat C = \frac{{{{180}^o} - {{120}^o}}}{2} = {30^o}\).
Xét tam giác ABM vuông tại A có:
\(\widehat {B} + \widehat {BAM} + \widehat {AMB} = {180^o}\\ \Rightarrow {30^o} + {90^o} + \widehat {AMB} = {180^o}\\ \Rightarrow \widehat {AMB} = {60^o}\\ \Rightarrow \widehat {AMC} = {180^o} - \widehat {AMB} = {180^o} - {60^o} = {120^o}\)
Xét tam giác MAC có:
\(\begin{array}{l}\widehat {AMC} + \widehat {MAC} + \widehat C = {180^o}\\ \Rightarrow {120^o} + \widehat {MAC} + {30^o} = {180^o}\\ \Rightarrow \widehat {MAC} = {30^o} = \widehat C\end{array}\)
\(\Rightarrow \) Tam giác AMC cân tại M.
Vì \(\Delta BAM = \Delta CAN\)
=> BM=CN ( 2 cạnh tương ứng)
=> BM+MN=CN+NM
=> BN=CM
Xét 2 tam giác ANB và AMC có:
AB=AC (cmt)
\(AN = AM\)(do \(\Delta BAM = \Delta CAN\))
BN=MC (cmt)
=>\(\Delta ANB = \Delta AMC\)(c.c.c)
Mà tam giác AMC cân tại M.
=> Tam giác ANB cân tại N.
Cách 2:
Xét tam giác ABC cân tại A, có \(\widehat {A{\rm{ }}} = 120^\circ \) có:
\(\widehat B = \widehat C = \frac{{{{180}^o} - {{120}^o}}}{2} = {30^o}\).
Xét tam giác ABM vuông tại A có:
\(\widehat B + \widehat {BAM} + \widehat {AMB} = {180^o}\\ \Rightarrow {30^o} + {90^o} + \widehat {AMB} = {180^o}\\ \Rightarrow \widehat {AMB} = {60^o}\)
Vì \(\Delta BAM = \Delta CAN\) nên AM = AN (2 cạnh tương ứng)
=> \(\Delta AMN\) đều (Tam giác cân có 1 góc bằng 60 độ)
=> \(\widehat {NAM}=60^0\)
Ta có: \(\widehat{BAN}+\widehat{NAM}=\widehat{BAM}\)
=> \(\widehat{BAN} + 60^0=90^0\)
=> \(\widehat{BAN}=30^0\)
Xét tam giác ABN có \(\widehat{BAN}=\widehat{ABN}(=30^0\) nên \(\Delta ABN\) cân tại N.
Ta có: \(\widehat{CAM}+\widehat{NAM}=\widehat{CAN}\)
=> \(\widehat{CAM} + 60^0=90^0\)
=> \(\widehat{CAM}=30^0\)
Xét tam giác ACM có \(\widehat{CAM}=\widehat{ACM}(=30^0\) nên \(\Delta ACM\) cân tại M.
Bài 4.38 trang 87 SGK Toán 7 tập 1 - Kết nối tri thức là một bài toán ứng dụng thực tế về các góc tạo bởi đường thẳng cắt đường thẳng. Để giải bài toán này, học sinh cần nắm vững các kiến thức sau:
Nội dung bài toán:
Cho hình vẽ (hình vẽ cần được mô tả chi tiết, ví dụ: hai đường thẳng a và b cắt nhau tại điểm O, có các góc được đánh số từ 1 đến 8). Biết góc AOB = 40 độ. Tính số đo của các góc còn lại.
Lời giải:
Kết luận:
Số đo của các góc còn lại là:
Để giải các bài toán về các góc tạo bởi đường thẳng cắt đường thẳng, học sinh cần:
Ví dụ minh họa:
Cho hai đường thẳng a và b cắt nhau tại điểm O. Biết góc AOB = 60 độ. Tính số đo của góc AOC.
Lời giải:
Vì góc AOB và góc AOC là hai góc kề bù nên góc AOC = 180 độ - góc AOB = 180 độ - 60 độ = 120 độ.
Để củng cố kiến thức về các góc tạo bởi đường thẳng cắt đường thẳng, các em học sinh có thể làm thêm các bài tập sau:
Giaitoan.edu.vn hy vọng với lời giải chi tiết và phương pháp giải bài 4.38 trang 87 SGK Toán 7 tập 1 - Kết nối tri thức trên đây, các em học sinh sẽ hiểu rõ hơn về bài toán và có thể tự tin giải các bài tập tương tự.
Chúc các em học tốt!