Giaitoan.edu.vn xin giới thiệu lời giải chi tiết mục 2 trang 61,62 sách giáo khoa Toán 7 tập 2 chương trình Kết nối tri thức. Bài viết này sẽ giúp học sinh nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi cung cấp đáp án chính xác, dễ hiểu, kèm theo các bước giải cụ thể, giúp các em học sinh có thể tự học tại nhà hoặc ôn tập kiến thức một cách hiệu quả.
Quan sát tam giác ABC trong Hình 9.4
Cho tam giác MNP có \(\widehat M = 47^\circ ;\widehat N = 53^\circ \). Hãy viết các cạnh của tam giác đó theo thứ tự độ dài từ bé đến lớn.
Phương pháp giải:
+ Áp dụng định lí tổng ba góc trong tam giác, tính góc còn lại của tam giác
+ Sử dụng định lí: Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn
Lời giải chi tiết:
Áp dụng định lí tổng ba góc trong một tam giác trong tam giác MNP, có:
\(\begin{array}{l}\widehat M + \widehat N + \widehat P = 180^\circ \\ \Rightarrow 47^\circ + 53^\circ + \widehat P = 180^\circ \\ \Rightarrow \widehat P = 180^\circ - 47^\circ - 53^\circ = 80^\circ \\ \Rightarrow \widehat M < \widehat N < \widehat P(47^\circ < 53^\circ < 80^\circ )\end{array}\)
\( \Rightarrow \) NP < MP < MN ( cạnh đối diện với góc lớn hơn thì lớn hơn)
Vậy các cạnh của tam giác đó theo thứ tự độ dài từ bé đến lớn là NP, MP, MN.
Em hãy so sánh độ dài hai cạnh AC và AB để kiểm tra lại dự đoán của mình trong HĐ3
Phương pháp giải:
Đo độ dài các cạnh rồi so sánh.
Lời giải chi tiết:
Đo độ dài các cạnh, ta được:
AB = 3,3 cm
AC = 4,6 cm
Do đó cạnh AC lớn hơn cạnh AB
Vậy dự đoán của em ở HĐ3 là đúng.
Trong trận bóng đá, trái bóng đang ở vị trí D, ba cầu thủ đứng thẳng hàng tại vị trí A, B, C trên sân với số áo lần lượt là 4, 2, 3 như Hình 9.1. Theo em cầu thủ nào gần trái bóng nhất, cầu thủ nào xa trái bóng nhất? Tại sao?
( Biết rằng góc ACD là góc tù)
Phương pháp giải:
Sử dụng định lí: Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn
Lời giải chi tiết:
Trong tam giác BCD, góc DCB là góc tù nên là góc lớn nhất. Cạnh DB đối diện với góc lớn nhất nên là cạnh lớn nhất
\( \Rightarrow \) DB > DC (1)
Vì góc DBA là góc ngoài tại đỉnh B của tam giác BCD nên \(\widehat {ABD} > \widehat {BCD}\)nên góc DBA cũng là góc tù.
Trong tam giác ABD, góc DCA là góc tù nên là góc lớn nhất. Cạnh DA đối diện với góc lớn nhất nên là cạnh lớn nhất
\( \Rightarrow \) DA > DB (2)
Từ (1) và (2) \( \Rightarrow \) DA > DB > DC
Vậy DA dài nhất, DC ngắn nhất
Do đó, cầu thủ C gần trái bóng nhất, cầu thủ A xa trái bóng nhất.
Quan sát tam giác ABC trong Hình 9.4
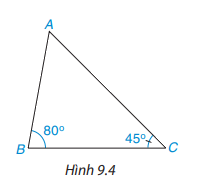
Em hãy dự đoán xem giữa hai cạnh đối diện với hai góc B và C ( tức là cạnh AC và AB) thì cạnh nào lớn hơn.
Phương pháp giải:
Quan sát, so sánh các cạnh
Lời giải chi tiết:
Em dự đoán cạnh đối diện với góc B lớn hơn cạnh đối diện với góc C.
Cho tam giác ABC có góc A là góc tù.

Theo em bạn nào nói đúng? Vì sao?
Phương pháp giải:
+ Góc tù là góc lớn nhất trong tam giác
+ Sử dụng định lí: Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn
Lời giải chi tiết:
Vì tam giác ABC có góc A là góc tù nên góc A là góc lớn nhất trong tam giác ABC.
\( \Rightarrow \) Cạnh đối diện với góc A là cạnh lớn nhất trong tam giác ABC.
Mà cạnh BC là cạnh đối diện với góc A
Vậy cạnh BC là cạnh lớn nhất trong tam giác ABC. Do đó bạn Tròn nói đúng.
Quan sát tam giác ABC trong Hình 9.4
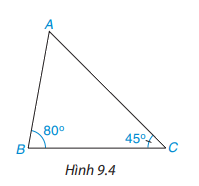
Em hãy dự đoán xem giữa hai cạnh đối diện với hai góc B và C ( tức là cạnh AC và AB) thì cạnh nào lớn hơn.
Phương pháp giải:
Quan sát, so sánh các cạnh
Lời giải chi tiết:
Em dự đoán cạnh đối diện với góc B lớn hơn cạnh đối diện với góc C.
Em hãy so sánh độ dài hai cạnh AC và AB để kiểm tra lại dự đoán của mình trong HĐ3
Phương pháp giải:
Đo độ dài các cạnh rồi so sánh.
Lời giải chi tiết:
Đo độ dài các cạnh, ta được:
AB = 3,3 cm
AC = 4,6 cm
Do đó cạnh AC lớn hơn cạnh AB
Vậy dự đoán của em ở HĐ3 là đúng.
Cho tam giác MNP có \(\widehat M = 47^\circ ;\widehat N = 53^\circ \). Hãy viết các cạnh của tam giác đó theo thứ tự độ dài từ bé đến lớn.
Phương pháp giải:
+ Áp dụng định lí tổng ba góc trong tam giác, tính góc còn lại của tam giác
+ Sử dụng định lí: Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn
Lời giải chi tiết:
Áp dụng định lí tổng ba góc trong một tam giác trong tam giác MNP, có:
\(\begin{array}{l}\widehat M + \widehat N + \widehat P = 180^\circ \\ \Rightarrow 47^\circ + 53^\circ + \widehat P = 180^\circ \\ \Rightarrow \widehat P = 180^\circ - 47^\circ - 53^\circ = 80^\circ \\ \Rightarrow \widehat M < \widehat N < \widehat P(47^\circ < 53^\circ < 80^\circ )\end{array}\)
\( \Rightarrow \) NP < MP < MN ( cạnh đối diện với góc lớn hơn thì lớn hơn)
Vậy các cạnh của tam giác đó theo thứ tự độ dài từ bé đến lớn là NP, MP, MN.
Cho tam giác ABC có góc A là góc tù.

Theo em bạn nào nói đúng? Vì sao?
Phương pháp giải:
+ Góc tù là góc lớn nhất trong tam giác
+ Sử dụng định lí: Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn
Lời giải chi tiết:
Vì tam giác ABC có góc A là góc tù nên góc A là góc lớn nhất trong tam giác ABC.
\( \Rightarrow \) Cạnh đối diện với góc A là cạnh lớn nhất trong tam giác ABC.
Mà cạnh BC là cạnh đối diện với góc A
Vậy cạnh BC là cạnh lớn nhất trong tam giác ABC. Do đó bạn Tròn nói đúng.
Trong trận bóng đá, trái bóng đang ở vị trí D, ba cầu thủ đứng thẳng hàng tại vị trí A, B, C trên sân với số áo lần lượt là 4, 2, 3 như Hình 9.1. Theo em cầu thủ nào gần trái bóng nhất, cầu thủ nào xa trái bóng nhất? Tại sao?
( Biết rằng góc ACD là góc tù)
Phương pháp giải:
Sử dụng định lí: Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn
Lời giải chi tiết:
Trong tam giác BCD, góc DCB là góc tù nên là góc lớn nhất. Cạnh DB đối diện với góc lớn nhất nên là cạnh lớn nhất
\( \Rightarrow \) DB > DC (1)
Vì góc DBA là góc ngoài tại đỉnh B của tam giác BCD nên \(\widehat {ABD} > \widehat {BCD}\)nên góc DBA cũng là góc tù.
Trong tam giác ABD, góc DCA là góc tù nên là góc lớn nhất. Cạnh DA đối diện với góc lớn nhất nên là cạnh lớn nhất
\( \Rightarrow \) DA > DB (2)
Từ (1) và (2) \( \Rightarrow \) DA > DB > DC
Vậy DA dài nhất, DC ngắn nhất
Do đó, cầu thủ C gần trái bóng nhất, cầu thủ A xa trái bóng nhất.
Mục 2 trang 61,62 SGK Toán 7 tập 2 - Kết nối tri thức tập trung vào việc ôn tập chương I: Các số hữu tỉ. Đây là một phần quan trọng giúp học sinh củng cố kiến thức về các khái niệm cơ bản như số hữu tỉ, số nguyên, số thập phân, phân số, và các phép toán trên chúng. Việc nắm vững kiến thức này là nền tảng cho các chương học tiếp theo.
Mục 2 bao gồm các bài tập vận dụng kiến thức đã học để giải quyết các bài toán thực tế. Các bài tập thường yêu cầu học sinh:
Bài 1 yêu cầu học sinh điền vào chỗ trống để hoàn thiện các câu phát biểu về số hữu tỉ. Để giải bài này, học sinh cần nắm vững định nghĩa về số hữu tỉ, số nguyên, số thập phân, phân số và các tính chất của chúng.
Ví dụ: Câu “Một số tự nhiên khác 0 luôn là một số…” cần được điền là “hữu tỉ”.
Bài 2 yêu cầu học sinh xác định các số hữu tỉ trong một tập hợp cho trước. Để giải bài này, học sinh cần nhớ lại định nghĩa về số hữu tỉ và kiểm tra xem mỗi phần tử trong tập hợp có thỏa mãn định nghĩa đó hay không.
Ví dụ: Số 3/4 là số hữu tỉ vì nó có thể biểu diễn dưới dạng phân số a/b, trong đó a và b là các số nguyên và b khác 0.
Bài 3 yêu cầu học sinh thực hiện các phép toán cộng, trừ, nhân, chia các số hữu tỉ. Để giải bài này, học sinh cần nắm vững các quy tắc thực hiện các phép toán trên số hữu tỉ, bao gồm quy tắc cộng, trừ hai số hữu tỉ cùng mẫu, khác mẫu, quy tắc nhân, chia hai số hữu tỉ.
Ví dụ: Để cộng hai số hữu tỉ 1/2 và 1/3, ta cần quy đồng mẫu số để đưa về cùng mẫu số chung là 6. Sau đó, ta cộng các tử số và giữ nguyên mẫu số: 1/2 + 1/3 = 3/6 + 2/6 = 5/6.
Bài 4 yêu cầu học sinh giải các bài toán có liên quan đến các ứng dụng của số hữu tỉ trong đời sống. Để giải bài này, học sinh cần đọc kỹ đề bài, xác định các thông tin quan trọng và sử dụng kiến thức về số hữu tỉ để giải quyết bài toán.
Ví dụ: Một bài toán có thể yêu cầu tính số tiền lãi khi gửi tiết kiệm với lãi suất là một số hữu tỉ. Học sinh cần sử dụng công thức tính lãi suất để giải quyết bài toán này.
Để học tốt môn Toán 7, đặc biệt là phần số hữu tỉ, học sinh cần:
Hy vọng rằng với lời giải chi tiết và hướng dẫn giải các bài tập trong mục 2 trang 61,62 SGK Toán 7 tập 2 - Kết nối tri thức, các em học sinh sẽ học tập hiệu quả và đạt kết quả tốt trong môn Toán.