Giaitoan.edu.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 3 trang 30, 31 sách giáo khoa Toán 7 tập 1 chương trình Kết nối tri thức. Bài viết này sẽ giúp các em học sinh nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi cung cấp đáp án đầy đủ, kèm theo các bước giải chi tiết, giúp các em dễ dàng theo dõi và áp dụng vào các bài tập tương tự.
Sử dụng máy tính cầm tay tính các căn bậc hai số học sau (làm tròn kết quả với độ chính xác 0,005, nếu cần).
Kim tự tháp Kheops là công trình kiến trúc nổi tiếng thế giới. Để xây dựng được công trình này, người ta phải sử dụng tới hơn 2,5 triệu mét khối đá, với diện tích đáy lên tới 52 198,16 m2.
(Theo khoahoc.tv)
Biết rằng đáy của kim tự tháp Kheops có dạng một hình vuông. Tính độ dài cạnh đáy của kim tự tháp này (làm tròn kết quả đến chữ số thập phân thứ nhất).
Phương pháp giải:
Tính cạnh a của hình vuông có diện tích S: \(a = \sqrt S \)
Làm tròn theo quy tắc làm tròn số thập phân.
- Đối với chữ số hàng làm tròn:
+ Giữ nguyên nếu chữ số ngay bên phải nhỏ hơn 5;
+Tăng 1 đơn vị nếu chữ số ngay bên phải lớn hơn hoặc bằng 5
- Đối với chữ số sau hàng làm tròn:
+ Bỏ đi nếu ở phần thập phân;
+ Thay bằng các chữ số 0 nếu ở phần số nguyên
Lời giải chi tiết:
Độ dài cạnh đáy của kim tự tháp này là: \(\sqrt {52198,16} \approx 228,469\)(m)
Làm tròn đến chữ số thập phân thứ nhất, ta được: 228,5 m (vì chữ số ở hàng làm tròn là 4, chữ số ngay sau hàng làm tròn là 6 > 5 nên ta tăng 1 đơn vị ở hàng làm tròn, đồng thời bỏ đi các chữ số ở sau hàng làm tròn)
Sử dụng máy tính cầm tay tính các căn bậc hai số học sau (làm tròn kết quả với độ chính xác 0,005, nếu cần).
\(a)\sqrt {15} ;b)\sqrt {2,56} ;c)\sqrt {17256} ;d)\sqrt {793881} \)
Phương pháp giải:
+ Bước 1: Bấm máy tính, tính các căn bậc hai.
+ Bước 2: Xác định hàng làm tròn.

+ Bước 3: Làm tròn theo quy tắc làm tròn số thập phân.
- Đối với chữ số hàng làm tròn:
+ Giữ nguyên nếu chữ số ngay bên phải nhỏ hơn 5;
+Tăng 1 đơn vị nếu chữ số ngay bên phải lớn hơn hoặc bằng 5
- Đối với chữ số sau hàng làm tròn:
+ Bỏ đi nếu ở phần thập phân;
+ Thay bằng các chữ số 0 nếu ở phần số nguyên
Lời giải chi tiết:
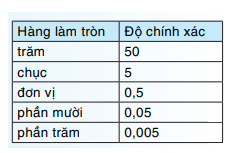
Độ chính xác 0,005 tức là ta cần làm tròn đến hàng phần trăm
\(a)\sqrt {15}=3,8729...\approx 3,87\\b)\sqrt {2,56} = 1,6\\c)\sqrt {17256} =131,3620... \approx 131,36\\d)\sqrt {793881} = 891\)
Sử dụng máy tính cầm tay tính các căn bậc hai số học sau (làm tròn kết quả với độ chính xác 0,005, nếu cần).
\(a)\sqrt {15} ;b)\sqrt {2,56} ;c)\sqrt {17256} ;d)\sqrt {793881} \)
Phương pháp giải:
+ Bước 1: Bấm máy tính, tính các căn bậc hai.
+ Bước 2: Xác định hàng làm tròn.
+ Bước 3: Làm tròn theo quy tắc làm tròn số thập phân.
- Đối với chữ số hàng làm tròn:
+ Giữ nguyên nếu chữ số ngay bên phải nhỏ hơn 5;
+Tăng 1 đơn vị nếu chữ số ngay bên phải lớn hơn hoặc bằng 5
- Đối với chữ số sau hàng làm tròn:
+ Bỏ đi nếu ở phần thập phân;
+ Thay bằng các chữ số 0 nếu ở phần số nguyên
Lời giải chi tiết:
Độ chính xác 0,005 tức là ta cần làm tròn đến hàng phần trăm
\(a)\sqrt {15}=3,8729...\approx 3,87\\b)\sqrt {2,56} = 1,6\\c)\sqrt {17256} =131,3620... \approx 131,36\\d)\sqrt {793881} = 891\)
Kim tự tháp Kheops là công trình kiến trúc nổi tiếng thế giới. Để xây dựng được công trình này, người ta phải sử dụng tới hơn 2,5 triệu mét khối đá, với diện tích đáy lên tới 52 198,16 m2.
(Theo khoahoc.tv)
Biết rằng đáy của kim tự tháp Kheops có dạng một hình vuông. Tính độ dài cạnh đáy của kim tự tháp này (làm tròn kết quả đến chữ số thập phân thứ nhất).
Phương pháp giải:
Tính cạnh a của hình vuông có diện tích S: \(a = \sqrt S \)
Làm tròn theo quy tắc làm tròn số thập phân.
- Đối với chữ số hàng làm tròn:
+ Giữ nguyên nếu chữ số ngay bên phải nhỏ hơn 5;
+Tăng 1 đơn vị nếu chữ số ngay bên phải lớn hơn hoặc bằng 5
- Đối với chữ số sau hàng làm tròn:
+ Bỏ đi nếu ở phần thập phân;
+ Thay bằng các chữ số 0 nếu ở phần số nguyên
Lời giải chi tiết:
Độ dài cạnh đáy của kim tự tháp này là: \(\sqrt {52198,16} \approx 228,469\)(m)
Làm tròn đến chữ số thập phân thứ nhất, ta được: 228,5 m (vì chữ số ở hàng làm tròn là 4, chữ số ngay sau hàng làm tròn là 6 > 5 nên ta tăng 1 đơn vị ở hàng làm tròn, đồng thời bỏ đi các chữ số ở sau hàng làm tròn)
Mục 3 trong SGK Toán 7 tập 1 Kết nối tri thức tập trung vào việc ôn tập và củng cố các kiến thức về số nguyên, số hữu tỉ, và các phép toán trên chúng. Đây là phần quan trọng để học sinh nắm vững nền tảng toán học, chuẩn bị cho các chương học tiếp theo. Việc giải các bài tập trong mục này không chỉ giúp học sinh hiểu rõ lý thuyết mà còn rèn luyện kỹ năng giải toán, tư duy logic và khả năng áp dụng kiến thức vào thực tế.
Mục 3 bao gồm các bài tập đa dạng, từ việc thực hiện các phép tính đơn giản đến việc giải các bài toán có tính ứng dụng cao. Các bài tập thường yêu cầu học sinh:
Bài tập 1 yêu cầu học sinh thực hiện các phép tính cộng, trừ số nguyên. Để giải bài tập này, học sinh cần nắm vững quy tắc cộng, trừ số nguyên:
Ví dụ: a) 3 + (-5) = -2; b) (-7) + 2 = -5; c) 4 - (-2) = 4 + 2 = 6
Bài tập 2 yêu cầu học sinh tìm giá trị tuyệt đối của các số nguyên. Giá trị tuyệt đối của một số nguyên là khoảng cách từ số đó đến số 0 trên trục số. Ký hiệu giá trị tuyệt đối của x là |x|.
Ví dụ: |3| = 3; |-5| = 5; |0| = 0
Bài tập 3 yêu cầu học sinh so sánh các số nguyên. Để so sánh các số nguyên, ta sử dụng các quy tắc sau:
Ví dụ: -5 < 2; -3 < -1; 4 > 1
Bài tập 4 thường là các bài toán ứng dụng liên quan đến số nguyên và số hữu tỉ. Để giải các bài toán này, học sinh cần đọc kỹ đề bài, xác định các yếu tố liên quan đến số nguyên và số hữu tỉ, và áp dụng các kiến thức đã học để giải quyết vấn đề.
Việc giải các bài tập trong mục 3 trang 30, 31 SGK Toán 7 tập 1 - Kết nối tri thức là một bước quan trọng trong quá trình học tập môn Toán của các em. Hy vọng với lời giải chi tiết và những lưu ý trên, các em sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong môn học này. Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục tri thức!