Chào mừng các em học sinh đến với lời giải chi tiết mục 1 trang 46, 47 sách giáo khoa Toán 7 tập 1 chương trình Kết nối tri thức. Bài viết này sẽ cung cấp đáp án đầy đủ và cách giải các bài tập trong mục, giúp các em hiểu rõ kiến thức và rèn luyện kỹ năng giải toán.
giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Chúng tôi cam kết mang đến những giải pháp học tập hiệu quả và chất lượng nhất.
Cho đường thẳng mn cắt đường thẳng xy và uv lần lượt tại hai điểm P và Q (H.3.17).Em hãy kể tên:.. Trên Hình 3.18, cho biết hai góc so le trong
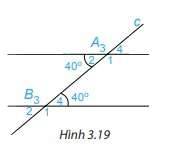
a) Cho hình 3.19, biết \(\widehat {{A_2}} = 40^\circ ;\widehat {{B_4}} = 40^\circ \). Em hãy cho biết số đo các góc còn lại.
b) Các cặp góc A1 và B4; A2 và B3 được gọi là các cặp góc trong cùng phía. Tính tổng: \(\widehat {{A_1}} + \widehat {{B_4}};\widehat {{A_2}} + \widehat {{B_3}}\).
Phương pháp giải:
Sử dụng tính chất: Tổng 2 góc kề bù bằng 180 độ hoặc 2 góc đối đỉnh thì bằng nhau
Đường thẳng c cắt 2 đường thẳng, tạo thành 1 cặp góc so le trong bằng nhau.
Lời giải chi tiết:
a) Vì \(\widehat {{A_1}} + \widehat {{A_2}} = 180^\circ \) (2 góc kề bù)
\( \Rightarrow \widehat {{A_1}} + 40^\circ = 180^\circ \)
\( \Rightarrow \widehat {{A_1}} = 180^\circ - 40^\circ = 140^\circ \)
Ta có: \(\widehat {{A_1}} = \widehat {{A_3}}\) (2 góc đối đỉnh), mà \(\widehat {{A_1}} = 140^\circ \) nên \(\widehat {{A_3}} = 140^\circ \)
\(\widehat {{A_2}} = \widehat {{A_4}}\)(2 góc đối đỉnh), mà \(\widehat {{A_2}} = 40^\circ \) nên \(\widehat {{A_4}} = 40^\circ \)
Vì \(\widehat {{A_2}} = \widehat {{B_4}} = 40^\circ \), mà 2 góc này ở vị trí so le trong
\( \Rightarrow \) 2 góc đồng vị bằng nhau nên
\(\begin{array}{l}\widehat {{A_1}} = \widehat {{B_1}} = 140^\circ ;\widehat {{A_2}} = \widehat {{B_2}} = 40^\circ ;\\\widehat {{A_3}} = \widehat {{B_3}} = 140^\circ ;\widehat {{A_4}} = \widehat {{B_4}} = 40^\circ \end{array}\)
b) Ta có:
\(\begin{array}{l}\widehat {{A_1}} + \widehat {{B_4}} = 140^\circ + 40^\circ = 180^\circ \\\widehat {{A_2}} + \widehat {{B_3}} = 40^\circ + 140^\circ = 180^\circ \end{array}\)
Trên Hình 3.18, cho biết hai góc so le trong A1 và B3 bằng nhau và bằng \(60^\circ \).
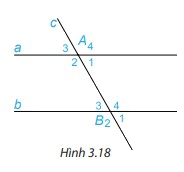
Hãy tính và so sánh hai góc so le trong còn lại A2 và B4.
Phương pháp giải:
Sử dụng tính chất 2 góc kề bù: Tổng 2 góc kề bù bằng 180 độ
Lời giải chi tiết:
+) Vì \(\widehat {{A_1}} + \widehat {{A_2}} = 180^\circ \) (2 góc kề bù)
\(\begin{array}{l} \Rightarrow 60^\circ + \widehat {{A_2}} = 180^\circ \\ \Rightarrow \widehat {{A_2}} = 180^\circ - 60^\circ = 120^\circ \end{array}\)
+) Vì \(\widehat {{B_3}} + \widehat {{B_4}} = 180^\circ \) (2 góc kề bù)
\(\begin{array}{l} \Rightarrow 60^\circ + \widehat {{B_4}} = 180^\circ \\ \Rightarrow \widehat {{B_4}} = 180^\circ - 60^\circ = 120^\circ \end{array}\)
Vậy hai góc so le trong còn lại A2 và B4 bằng nhau và bằng \(120^\circ \).
Trên Hình 3.18, cho biết hai góc so le trong A1 và B3 bằng nhau và bằng \(60^\circ \).
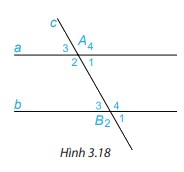
Chọn hai góc đồng vị rồi tính và so sánh hai góc đó.
Phương pháp giải:
Sử dụng tính chất: Tổng 2 góc kề bù bằng 180 độ hoặc 2 góc đối đỉnh thì bằng nhau
Lời giải chi tiết:
Chọn cặp góc đồng vị: góc A1 và góc B1
Ta có: \(\widehat {{A_1}} = 60^\circ ;\widehat {{B_3}} = 60^\circ \)
\(\widehat {{B_1}} = \widehat {{B_3}}\) (2 góc đối đỉnh)
\( \Rightarrow \widehat {{B_1}} = 60^\circ \)
Vậy hai góc A1 và góc B1 đồng vị bằng nhau và bằng \(60^0\)
Cho đường thẳng mn cắt đường thẳng xy và uv lần lượt tại hai điểm P và Q (H.3.17).Em hãy kể tên:
a) Hai cặp góc so le trong
b) Bốn cặp góc đồng vị.
Phương pháp giải:
Vẽ hình, nhận diện các cặp góc so le trong, đồng vị.
Lời giải chi tiết:
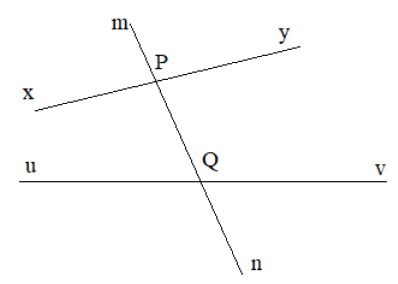
a) Hai cặp góc so le trong là: góc xPn và góc mQv; góc yPn và góc uQm
b) Bốn cặp góc đồng vị là: góc mPy và góc mQv; góc yPn và góc vQn; góc mPx và góc mQu; góc xPn và góc uQn.
Cho đường thẳng mn cắt đường thẳng xy và uv lần lượt tại hai điểm P và Q (H.3.17).Em hãy kể tên:
a) Hai cặp góc so le trong
b) Bốn cặp góc đồng vị.
Phương pháp giải:
Vẽ hình, nhận diện các cặp góc so le trong, đồng vị.
Lời giải chi tiết:
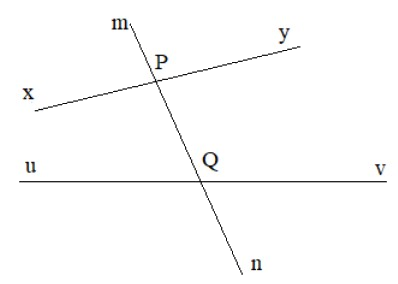
a) Hai cặp góc so le trong là: góc xPn và góc mQv; góc yPn và góc uQm
b) Bốn cặp góc đồng vị là: góc mPy và góc mQv; góc yPn và góc vQn; góc mPx và góc mQu; góc xPn và góc uQn.
Trên Hình 3.18, cho biết hai góc so le trong A1 và B3 bằng nhau và bằng \(60^\circ \).
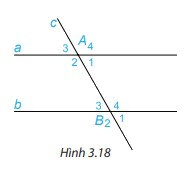
Hãy tính và so sánh hai góc so le trong còn lại A2 và B4.
Phương pháp giải:
Sử dụng tính chất 2 góc kề bù: Tổng 2 góc kề bù bằng 180 độ
Lời giải chi tiết:
+) Vì \(\widehat {{A_1}} + \widehat {{A_2}} = 180^\circ \) (2 góc kề bù)
\(\begin{array}{l} \Rightarrow 60^\circ + \widehat {{A_2}} = 180^\circ \\ \Rightarrow \widehat {{A_2}} = 180^\circ - 60^\circ = 120^\circ \end{array}\)
+) Vì \(\widehat {{B_3}} + \widehat {{B_4}} = 180^\circ \) (2 góc kề bù)
\(\begin{array}{l} \Rightarrow 60^\circ + \widehat {{B_4}} = 180^\circ \\ \Rightarrow \widehat {{B_4}} = 180^\circ - 60^\circ = 120^\circ \end{array}\)
Vậy hai góc so le trong còn lại A2 và B4 bằng nhau và bằng \(120^\circ \).
Trên Hình 3.18, cho biết hai góc so le trong A1 và B3 bằng nhau và bằng \(60^\circ \).
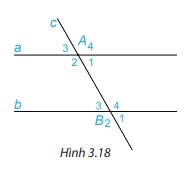
Chọn hai góc đồng vị rồi tính và so sánh hai góc đó.
Phương pháp giải:
Sử dụng tính chất: Tổng 2 góc kề bù bằng 180 độ hoặc 2 góc đối đỉnh thì bằng nhau
Lời giải chi tiết:
Chọn cặp góc đồng vị: góc A1 và góc B1
Ta có: \(\widehat {{A_1}} = 60^\circ ;\widehat {{B_3}} = 60^\circ \)
\(\widehat {{B_1}} = \widehat {{B_3}}\) (2 góc đối đỉnh)
\( \Rightarrow \widehat {{B_1}} = 60^\circ \)
Vậy hai góc A1 và góc B1 đồng vị bằng nhau và bằng \(60^0\)
a) Cho hình 3.19, biết \(\widehat {{A_2}} = 40^\circ ;\widehat {{B_4}} = 40^\circ \). Em hãy cho biết số đo các góc còn lại.
b) Các cặp góc A1 và B4; A2 và B3 được gọi là các cặp góc trong cùng phía. Tính tổng: \(\widehat {{A_1}} + \widehat {{B_4}};\widehat {{A_2}} + \widehat {{B_3}}\).
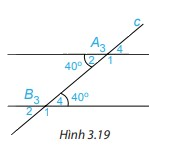
Phương pháp giải:
Sử dụng tính chất: Tổng 2 góc kề bù bằng 180 độ hoặc 2 góc đối đỉnh thì bằng nhau
Đường thẳng c cắt 2 đường thẳng, tạo thành 1 cặp góc so le trong bằng nhau.
Lời giải chi tiết:
a) Vì \(\widehat {{A_1}} + \widehat {{A_2}} = 180^\circ \) (2 góc kề bù)
\( \Rightarrow \widehat {{A_1}} + 40^\circ = 180^\circ \)
\( \Rightarrow \widehat {{A_1}} = 180^\circ - 40^\circ = 140^\circ \)
Ta có: \(\widehat {{A_1}} = \widehat {{A_3}}\) (2 góc đối đỉnh), mà \(\widehat {{A_1}} = 140^\circ \) nên \(\widehat {{A_3}} = 140^\circ \)
\(\widehat {{A_2}} = \widehat {{A_4}}\)(2 góc đối đỉnh), mà \(\widehat {{A_2}} = 40^\circ \) nên \(\widehat {{A_4}} = 40^\circ \)
Vì \(\widehat {{A_2}} = \widehat {{B_4}} = 40^\circ \), mà 2 góc này ở vị trí so le trong
\( \Rightarrow \) 2 góc đồng vị bằng nhau nên
\(\begin{array}{l}\widehat {{A_1}} = \widehat {{B_1}} = 140^\circ ;\widehat {{A_2}} = \widehat {{B_2}} = 40^\circ ;\\\widehat {{A_3}} = \widehat {{B_3}} = 140^\circ ;\widehat {{A_4}} = \widehat {{B_4}} = 40^\circ \end{array}\)
b) Ta có:
\(\begin{array}{l}\widehat {{A_1}} + \widehat {{B_4}} = 140^\circ + 40^\circ = 180^\circ \\\widehat {{A_2}} + \widehat {{B_3}} = 40^\circ + 140^\circ = 180^\circ \end{array}\)
Mục 1 trang 46, 47 SGK Toán 7 tập 1 - Kết nối tri thức tập trung vào việc ôn tập và củng cố các kiến thức về số hữu tỉ, phép cộng, trừ, nhân, chia số hữu tỉ. Các bài tập trong mục này giúp học sinh rèn luyện kỹ năng thực hiện các phép toán với số hữu tỉ, so sánh số hữu tỉ và áp dụng các tính chất của phép toán để giải quyết các bài toán thực tế.
Bài tập này yêu cầu học sinh thực hiện các phép tính cộng, trừ, nhân, chia số hữu tỉ. Để giải bài tập này, học sinh cần nắm vững các quy tắc thực hiện các phép toán với số hữu tỉ, bao gồm:
Ví dụ:
Tính: 1/2 + 2/3
Giải:
1/2 + 2/3 = 3/6 + 4/6 = 7/6
Bài tập này yêu cầu học sinh so sánh các số hữu tỉ. Để giải bài tập này, học sinh có thể sử dụng các phương pháp sau:
Ví dụ:
So sánh: 1/2 và 2/3
Giải:
1/2 = 3/6 và 2/3 = 4/6. Vì 3/6 < 4/6 nên 1/2 < 2/3
Bài tập này yêu cầu học sinh tìm giá trị của x thỏa mãn một phương trình hoặc bất phương trình. Để giải bài tập này, học sinh cần áp dụng các quy tắc biến đổi phương trình hoặc bất phương trình để đưa về dạng đơn giản và tìm ra giá trị của x.
Ví dụ:
Tìm x biết: x + 1/2 = 3/4
Giải:
x = 3/4 - 1/2 = 3/4 - 2/4 = 1/4
Kiến thức về số hữu tỉ và các phép toán với số hữu tỉ có ứng dụng rộng rãi trong đời sống thực tế, ví dụ như:
Hy vọng rằng với lời giải chi tiết và hướng dẫn cụ thể trong bài viết này, các em học sinh đã có thể tự tin giải quyết các bài tập trong mục 1 trang 46, 47 SGK Toán 7 tập 1 - Kết nối tri thức. Chúc các em học tập tốt!