Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 7. Trong bài viết này, chúng tôi sẽ cùng bạn giải quyết mục 1 trang 72 SGK Toán 7 tập 2 - Kết nối tri thức. Mục tiêu của chúng tôi là giúp bạn nắm vững kiến thức và tự tin giải các bài tập Toán học.
Mỗi tam giác có mấy đường trung tuyến?
Mỗi tam giác có mấy đường trung tuyến?
Phương pháp giải:
Đoạn thẳng nối đỉnh của tam giác với trung điểm cạnh đối diện được gọi là một đường trung tuyến của tam giác.
Lời giải chi tiết:
Tương ứng với mỗi đỉnh của tam giác có 1 đường trung tuyến nên mỗi tam giác có 3 đường trung tuyến.
Trên mảnh giấy kẻ ô vuông, mỗi chiều 10 ô, hãy đếm dòng, đánh dấu các đỉnh A,B,C rồi vẽ tam giác ABC. (H.9.29)
Vẽ hai đường trung tuyến BN, CP, chúng cát nhau tại G, tia AG cắt cạnh BC tại M.
Phương pháp giải:
Lời giải chi tiết:
Do đó, AM có là đường trung tuyến của tam giác ABC
\(\begin{array}{l}\dfrac{{GA}}{{MA}} = \dfrac{6}{9} = \dfrac{2}{3};\\\dfrac{{GB}}{{NB}} = \dfrac{2}{3};\\\dfrac{{GC}}{{PC}} = \dfrac{2}{3}\end{array}\)
Trong tình huống mở đầu, người ta chứng minh được G chính là trọng tâm của tam giác ABC. Em hãy cắt một mảnh bìa hình tam giác. Xác định trọng tâm của tam giác và đặt mảnh bìa đó lên một giá nhọn tại trọng tâm vừa xác định. Quan sát xem mảnh bìa có thăng bằng không
Phương pháp giải:
Bước 1: Cắt mảnh bìa hình tam giác.
Bước 2: Kẻ 2 đường trung tuyến của tam giác ABC, chúng cắt nhau tại G.
Bước 3: Đặt mảnh bìa đó lên một giá nhọn tại trọng tâm G.
Lời giải chi tiết:
Cắt mảnh bìa hình tam giác. Kẻ 2 đường trung tuyến của tam giác ABC, chúng cắt nhau tại G.
Đặt mảnh bìa đó lên một giá nhọn tại trọng tâm G thì thấy mảnh bìa thăng bằng.
Trong tam giác ABC ở ví dụ 1, cho trung tuyến BN và GN = 1 cm. Tính GB và NB.
Phương pháp giải:
Sử dụng định lí về sự đồng quy của ba đường trung tuyến của tam giác.
Lời giải chi tiết:
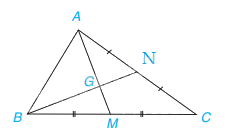
Vì G là trọng tâm của tam giác ABC nên \(\dfrac{{GB}}{{NB}} = \dfrac{2}{3} \Leftrightarrow GB = \dfrac{2}{3}NB\)
Ta có: GN = NB – GB = \(NB - \dfrac{2}{3}NB = \dfrac{1}{3}NB\)
Mà GN = 1 cm nên 1 = \(\dfrac{1}{3}.NB \Rightarrow NB = 3\)( cm)
\(GB = \dfrac{2}{3}NB = \dfrac{2}{3}.3 = 2\) ( cm)
Vậy GB = 2 cm, NB = 3 cm.
Hãy lấy một mảnh giấy hình tam giác, gấp giấy đánh dấu trung điểm của các cạnh. Sau đó, gấp giấy để được các nếp gấp đi qua đỉnh và trung điểm của cạnh đối diện ( tức là các đường trung tuyến của tam giác). Mở tờ giấy ra, quan sát và cho biết ba nếp gấp ( ba đường trung tuyến) có cùng đi qua một điểm không?

Phương pháp giải:
Gấp theo hướng dẫn
Lời giải chi tiết:
Ba nếp gấp đi qua cùng một điểm.

Phương pháp giải:
Sử dụng định lí về sự đồng quy của ba đường trung tuyến của tam giác.
Lời giải chi tiết:
Cách 1: Tìm giao điểm của 2 đường trung tuyến.
Cách 2: Vẽ 1 đường trung tuyến. Lấy điểm G cách đỉnh một khoảng bằng \(\dfrac{2}{3}\)độ dài đường trung tuyến đi qua đỉnh đó. Ta được G là trọng tâm tam giác.
1. Sự đồng quy của ba đường trung tuyến trong một tam giác
Mỗi tam giác có mấy đường trung tuyến?
Phương pháp giải:
Đoạn thẳng nối đỉnh của tam giác với trung điểm cạnh đối diện được gọi là một đường trung tuyến của tam giác.
Lời giải chi tiết:
Tương ứng với mỗi đỉnh của tam giác có 1 đường trung tuyến nên mỗi tam giác có 3 đường trung tuyến.
Hãy lấy một mảnh giấy hình tam giác, gấp giấy đánh dấu trung điểm của các cạnh. Sau đó, gấp giấy để được các nếp gấp đi qua đỉnh và trung điểm của cạnh đối diện ( tức là các đường trung tuyến của tam giác). Mở tờ giấy ra, quan sát và cho biết ba nếp gấp ( ba đường trung tuyến) có cùng đi qua một điểm không?

Phương pháp giải:
Gấp theo hướng dẫn
Lời giải chi tiết:
Ba nếp gấp đi qua cùng một điểm.
Trên mảnh giấy kẻ ô vuông, mỗi chiều 10 ô, hãy đếm dòng, đánh dấu các đỉnh A,B,C rồi vẽ tam giác ABC. (H.9.29)
Vẽ hai đường trung tuyến BN, CP, chúng cát nhau tại G, tia AG cắt cạnh BC tại M.
Phương pháp giải:
Lời giải chi tiết:
Do đó, AM có là đường trung tuyến của tam giác ABC
\(\begin{array}{l}\dfrac{{GA}}{{MA}} = \dfrac{6}{9} = \dfrac{2}{3};\\\dfrac{{GB}}{{NB}} = \dfrac{2}{3};\\\dfrac{{GC}}{{PC}} = \dfrac{2}{3}\end{array}\)
Trong tam giác ABC ở ví dụ 1, cho trung tuyến BN và GN = 1 cm. Tính GB và NB.
Phương pháp giải:
Sử dụng định lí về sự đồng quy của ba đường trung tuyến của tam giác.
Lời giải chi tiết:
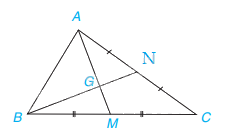
Vì G là trọng tâm của tam giác ABC nên \(\dfrac{{GB}}{{NB}} = \dfrac{2}{3} \Leftrightarrow GB = \dfrac{2}{3}NB\)
Ta có: GN = NB – GB = \(NB - \dfrac{2}{3}NB = \dfrac{1}{3}NB\)
Mà GN = 1 cm nên 1 = \(\dfrac{1}{3}.NB \Rightarrow NB = 3\)( cm)
\(GB = \dfrac{2}{3}NB = \dfrac{2}{3}.3 = 2\) ( cm)
Vậy GB = 2 cm, NB = 3 cm.

Phương pháp giải:
Sử dụng định lí về sự đồng quy của ba đường trung tuyến của tam giác.
Lời giải chi tiết:
Cách 1: Tìm giao điểm của 2 đường trung tuyến.
Cách 2: Vẽ 1 đường trung tuyến. Lấy điểm G cách đỉnh một khoảng bằng \(\dfrac{2}{3}\)độ dài đường trung tuyến đi qua đỉnh đó. Ta được G là trọng tâm tam giác.
Trong tình huống mở đầu, người ta chứng minh được G chính là trọng tâm của tam giác ABC. Em hãy cắt một mảnh bìa hình tam giác. Xác định trọng tâm của tam giác và đặt mảnh bìa đó lên một giá nhọn tại trọng tâm vừa xác định. Quan sát xem mảnh bìa có thăng bằng không
Phương pháp giải:
Bước 1: Cắt mảnh bìa hình tam giác.
Bước 2: Kẻ 2 đường trung tuyến của tam giác ABC, chúng cắt nhau tại G.
Bước 3: Đặt mảnh bìa đó lên một giá nhọn tại trọng tâm G.
Lời giải chi tiết:
Cắt mảnh bìa hình tam giác. Kẻ 2 đường trung tuyến của tam giác ABC, chúng cắt nhau tại G.
Đặt mảnh bìa đó lên một giá nhọn tại trọng tâm G thì thấy mảnh bìa thăng bằng.
Mục 1 trang 72 SGK Toán 7 tập 2 - Kết nối tri thức thường xoay quanh các kiến thức về biểu thức đại số, các phép toán trên biểu thức, và ứng dụng của chúng vào giải quyết các bài toán thực tế. Việc nắm vững kiến thức nền tảng là vô cùng quan trọng để giải quyết các bài tập một cách hiệu quả.
Để hiểu rõ hơn về Mục 1 trang 72, chúng ta cần xem xét các nội dung chính sau:
Dưới đây là một số bài tập minh họa thường gặp trong Mục 1 trang 72 SGK Toán 7 tập 2 - Kết nối tri thức, kèm theo lời giải chi tiết:
Cho biểu thức A = 3x + 2y. Tính giá trị của A khi x = 2 và y = -1.
Lời giải:
Thay x = 2 và y = -1 vào biểu thức A, ta có:
A = 3 * 2 + 2 * (-1) = 6 - 2 = 4
Vậy, giá trị của biểu thức A khi x = 2 và y = -1 là 4.
Rút gọn biểu thức B = 5x - 3x + 2x - 1.
Lời giải:
B = (5x - 3x + 2x) - 1 = (5 - 3 + 2)x - 1 = 4x - 1
Vậy, biểu thức B sau khi rút gọn là 4x - 1.
Một cửa hàng bán được x sản phẩm trong một ngày. Giá mỗi sản phẩm là y đồng. Tính tổng số tiền mà cửa hàng thu được trong một ngày.
Lời giải:
Tổng số tiền mà cửa hàng thu được trong một ngày là x * y đồng.
Để giải các bài tập trong Mục 1 trang 72 SGK Toán 7 tập 2 - Kết nối tri thức một cách hiệu quả, bạn có thể áp dụng một số mẹo sau:
Ngoài SGK Toán 7 tập 2 - Kết nối tri thức, bạn có thể tham khảo thêm các tài liệu sau để học Toán 7 hiệu quả hơn:
Hy vọng rằng, với những kiến thức và lời giải chi tiết trong bài viết này, bạn đã nắm vững cách giải Mục 1 trang 72 SGK Toán 7 tập 2 - Kết nối tri thức. Chúc bạn học tập tốt và đạt kết quả cao trong môn Toán!