Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 7 tập 2 Kết nối tri thức của giaitoan.edu.vn. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong sách giáo khoa, giúp các em nắm vững kiến thức và tự tin hơn trong học tập.
Trang 66, 67, 68 SGK Toán 7 tập 2 tập trung vào các chủ đề quan trọng như biểu thức đại số, thu gọn biểu thức, và các bài toán thực tế ứng dụng.
Cho hai bộ ba thanh tre nhỏ có độ dài như sau: Bộ thứ nhất: 10 cm, 20 cm, 25 cm. Bộ thứ hai: 5 cm, 15 cm, 25 cm. Em hãy ghép và cho biết bộ nào ghép được thành một tam giác.
Với bộ ba thanh tre ghép lại được thành một tam giác trong HĐ1, em hãy so sánh độ dài của thanh tre bất kì với tổng độ dài 2 thanh còn lại
Phương pháp giải:
Tính tổng độ dài của 2 thanh tre bất kì rồi so sánh với dộ dài thanh còn lại.
Lời giải chi tiết:
Ta có: 10 + 20 = 30 > 25
10 + 25 = 35 > 20
20 + 25 = 45 > 10
Vậy độ dài của thanh tre bất kì luôn nhỏ hơn tổng độ dài 2 thanh còn lại.
Trở lại tình huống mở đầu, em hãy giải thích vì sao nếu dựng cột điện ở vị trí C trên đoạn thẳng AB thì tổng độ dài dây dẫn điện cần sử dụng là ngắn nhất? (H.9.17)
Phương pháp giải:
Sử dụng bất đẳng thức tam giác: Trong một tam giác, độ dài của một cạnh luôn nhỏ hơn tổng độ dài hai cạnh còn lại.
Lời giải chi tiết:
+) Nếu A,B,C không thẳng hàng thì ta lập được tam giác ABC. Khi đó, theo bất đẳng thức tam giác, ta có:
AC + CB > AB, tức là độ dài dây dẫn luôn lớn hơn AB.
+) Nếu A,B,C thẳng hàng thì C nằm giữa A và B nên AC + CB = AB, tức là độ dài dây dẫn bằng AB.
Vậy khi C nằm trên đoạn thẳng AB thì tổng độ dài dây dẫn điện cần sử dụng là ngắn nhất.
Cho hai bộ ba thanh tre nhỏ có độ dài như sau:
Bộ thứ nhất: 10 cm, 20 cm, 25 cm.
Bộ thứ hai: 5 cm, 15 cm, 25 cm.
Em hãy ghép và cho biết bộ nào ghép được thành một tam giác.
Phương pháp giải:
Ghép sao cho cứ 2 đầu của 2 thanh tre trùng nhau thì bộ ba đó ghép được thành tam giác.
Lời giải chi tiết:
Bộ thứ nhất ghép được thành tam giác.
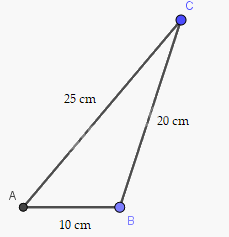
Hỏi ba độ dài nào sau đây không thể là độ dài ba cạnh của một tam giác? Vì sao? Hãy vẽ tam giác nhận ba độ dài còn lại làm độ dài 3 cạnh.
a) 5 cm, 4 cm, 6 cm.
b) 3 cm, 6 cm, 10 cm.
Phương pháp giải:
Khi kiểm tra 3 đoạn thẳng có thỏa mãn bất đẳng thức tam giác không, để nhanh gọn, ta chỉ cần kiểm tra tổng độ dài của 2 cạnh nhỏ hơn có lớn hơn độ dài cạnh lớn nhất hay không
Lời giải chi tiết:
a) Vì 5+4 > 6 nên ba độ dài 5 cm, 4 cm, 6 cm có thể là độ dài ba cạnh của một tam giác.
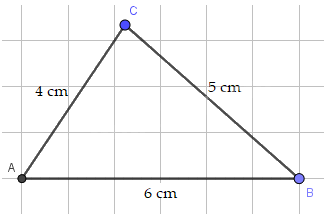
b) Vì 3 + 6 = 9 < 10 nên ba độ dài 3 cm, 6 cm, 10 cm không thể là độ dài ba cạnh của một tam giác

Ý kiến của em thì sao?
Phương pháp giải:
Sử dụng bất đẳng thức tam giác: Trong một tam giác, độ dài của một cạnh luôn nhỏ hơn tổng độ dài hai cạnh còn lại.
Kiểm tra, nếu ba độ dài không thỏa mãn bất đẳng thức tam giác thì chúng không ghép được thành một tam giác.
Lời giải chi tiết:
Vì 1+ 2 < 4 nên bộ ba đoạn thẳng không lập được thành 1 tam giác.
Vậy Vuông sai, Tròn đúng.
Chú ý: Khi kiểm tra 3 đoạn thẳng có thỏa mãn bất đẳng thức tam giác không, để nhanh gọn, ta chỉ cần kiểm tra tổng độ dài của 2 cạnh nhỏ hơn có lớn hơn độ dài cạnh lớn nhất hay không
Cho hai bộ ba thanh tre nhỏ có độ dài như sau:
Bộ thứ nhất: 10 cm, 20 cm, 25 cm.
Bộ thứ hai: 5 cm, 15 cm, 25 cm.
Em hãy ghép và cho biết bộ nào ghép được thành một tam giác.
Phương pháp giải:
Ghép sao cho cứ 2 đầu của 2 thanh tre trùng nhau thì bộ ba đó ghép được thành tam giác.
Lời giải chi tiết:
Bộ thứ nhất ghép được thành tam giác.
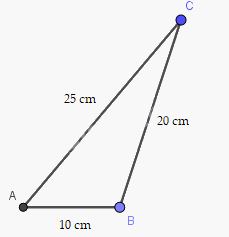
Với bộ ba thanh tre ghép lại được thành một tam giác trong HĐ1, em hãy so sánh độ dài của thanh tre bất kì với tổng độ dài 2 thanh còn lại
Phương pháp giải:
Tính tổng độ dài của 2 thanh tre bất kì rồi so sánh với dộ dài thanh còn lại.
Lời giải chi tiết:
Ta có: 10 + 20 = 30 > 25
10 + 25 = 35 > 20
20 + 25 = 45 > 10
Vậy độ dài của thanh tre bất kì luôn nhỏ hơn tổng độ dài 2 thanh còn lại.

Ý kiến của em thì sao?
Phương pháp giải:
Sử dụng bất đẳng thức tam giác: Trong một tam giác, độ dài của một cạnh luôn nhỏ hơn tổng độ dài hai cạnh còn lại.
Kiểm tra, nếu ba độ dài không thỏa mãn bất đẳng thức tam giác thì chúng không ghép được thành một tam giác.
Lời giải chi tiết:
Vì 1+ 2 < 4 nên bộ ba đoạn thẳng không lập được thành 1 tam giác.
Vậy Vuông sai, Tròn đúng.
Chú ý: Khi kiểm tra 3 đoạn thẳng có thỏa mãn bất đẳng thức tam giác không, để nhanh gọn, ta chỉ cần kiểm tra tổng độ dài của 2 cạnh nhỏ hơn có lớn hơn độ dài cạnh lớn nhất hay không
Hỏi ba độ dài nào sau đây không thể là độ dài ba cạnh của một tam giác? Vì sao? Hãy vẽ tam giác nhận ba độ dài còn lại làm độ dài 3 cạnh.
a) 5 cm, 4 cm, 6 cm.
b) 3 cm, 6 cm, 10 cm.
Phương pháp giải:
Khi kiểm tra 3 đoạn thẳng có thỏa mãn bất đẳng thức tam giác không, để nhanh gọn, ta chỉ cần kiểm tra tổng độ dài của 2 cạnh nhỏ hơn có lớn hơn độ dài cạnh lớn nhất hay không
Lời giải chi tiết:
a) Vì 5+4 > 6 nên ba độ dài 5 cm, 4 cm, 6 cm có thể là độ dài ba cạnh của một tam giác.
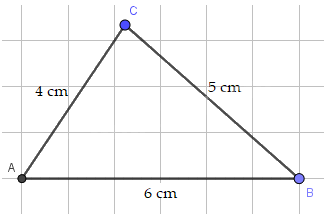
b) Vì 3 + 6 = 9 < 10 nên ba độ dài 3 cm, 6 cm, 10 cm không thể là độ dài ba cạnh của một tam giác
Trở lại tình huống mở đầu, em hãy giải thích vì sao nếu dựng cột điện ở vị trí C trên đoạn thẳng AB thì tổng độ dài dây dẫn điện cần sử dụng là ngắn nhất? (H.9.17)
Phương pháp giải:
Sử dụng bất đẳng thức tam giác: Trong một tam giác, độ dài của một cạnh luôn nhỏ hơn tổng độ dài hai cạnh còn lại.
Lời giải chi tiết:
+) Nếu A,B,C không thẳng hàng thì ta lập được tam giác ABC. Khi đó, theo bất đẳng thức tam giác, ta có:
AC + CB > AB, tức là độ dài dây dẫn luôn lớn hơn AB.
+) Nếu A,B,C thẳng hàng thì C nằm giữa A và B nên AC + CB = AB, tức là độ dài dây dẫn bằng AB.
Vậy khi C nằm trên đoạn thẳng AB thì tổng độ dài dây dẫn điện cần sử dụng là ngắn nhất.
Chương trình Toán 7 tập 2 Kết nối tri thức tiếp tục xây dựng nền tảng đại số, mở rộng các khái niệm về biểu thức đại số, phương trình bậc nhất một ẩn, và các ứng dụng thực tế. Trang 66, 67, 68 tập trung vào việc rèn luyện kỹ năng thu gọn biểu thức, tính giá trị của biểu thức, và giải các bài toán liên quan đến các tình huống thực tế.
Bài tập này yêu cầu học sinh áp dụng các quy tắc về dấu ngoặc, quy tắc chuyển vế, và các phép toán cộng, trừ, nhân, chia để thu gọn các biểu thức đại số cho trước. Việc thu gọn biểu thức giúp đơn giản hóa biểu thức, dễ dàng tính toán và so sánh.
Bài tập này yêu cầu học sinh thay các giá trị cụ thể của các biến vào biểu thức đại số đã thu gọn và tính giá trị của biểu thức. Đây là bước quan trọng để hiểu rõ mối liên hệ giữa các biến và giá trị của biểu thức.
Bài tập này yêu cầu học sinh sử dụng các kiến thức về biểu thức đại số để giải các bài toán liên quan đến các tình huống thực tế, như tính diện tích, chu vi, hoặc số tiền. Điều này giúp học sinh hiểu rõ hơn về ứng dụng của toán học trong cuộc sống.
Ví dụ: Một hình chữ nhật có chiều dài là 5cm và chiều rộng là 3cm. Hãy viết biểu thức tính chu vi của hình chữ nhật đó.
Lời giải: Chu vi của hình chữ nhật là 2(chiều dài + chiều rộng) = 2(5 + 3) = 2(8) = 16cm
Khi thu gọn biểu thức đại số, cần chú ý đến các quy tắc về dấu ngoặc và quy tắc chuyển vế. Khi tính giá trị của biểu thức, cần thay đúng giá trị của các biến và thực hiện các phép toán theo đúng thứ tự. Việc luyện tập thường xuyên sẽ giúp các em nắm vững kiến thức và tự tin hơn trong giải bài tập.
| Công thức | Mô tả |
|---|---|
| a + b = b + a | Tính giao hoán của phép cộng |
| a * b = b * a | Tính giao hoán của phép nhân |
| a + (b + c) = (a + b) + c | Tính kết hợp của phép cộng |
| a * (b * c) = (a * b) * c | Tính kết hợp của phép nhân |
| a * (b + c) = a * b + a * c | Tính chất phân phối của phép nhân đối với phép cộng |
Hy vọng với những hướng dẫn chi tiết và bài giải cụ thể trên đây, các em học sinh sẽ tự tin hơn trong việc giải các bài tập trang 66, 67, 68 SGK Toán 7 tập 2 Kết nối tri thức. Chúc các em học tập tốt và đạt kết quả cao!