Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 7 tại giaitoan.edu.vn. Bài viết này sẽ cung cấp lời giải chi tiết và dễ hiểu cho mục 1 trang 80, 81 sách giáo khoa Toán 7 tập 1 chương trình Kết nối tri thức.
Chúng tôi hiểu rằng việc tự học và làm bài tập đôi khi gặp nhiều khó khăn. Vì vậy, đội ngũ giaitoan.edu.vn đã biên soạn bài giải này với mục đích giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Hãy nêu tên tất cả các tam giác cân trong Hình 4.59. Với mỗi tam cân đó, hãy nêu tên cạnh bên, cạnh đáy, góc ở đỉnh, góc ở đáy của chúng.
Thử thách nhỏ
Một tam giác có gì đặc biệt nếu thoả mãn một trong các điều kiện sau:
a) Tam giác có ba góc bằng nhau?
b) Tam giác cân có một góc bằng 60°?
Phương pháp giải:
Áp dụng: Tam giác đều là tam giác có 3 cạnh bằng nhau hoặc ba góc bằng nhau.
Lời giải chi tiết:
a) Tam giác có ba góc bằng nhau là tam giác đều
b) Tam giác cân có 1 góc bằng 60 độ là tam giác đều.
Quan sát tam giác ABC cân tại A như Hình 4.60. Lấy D là trung điểm của đoạn thẳng BC.
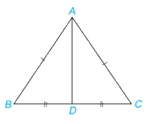
a) Chứng minh rằng \(\Delta \) ABD = \(\Delta \) ACD theo trường hợp cạnh - cạnh - cạnh.
b) Hai góc B và C của tam giác ABC có bằng nhau không?
Phương pháp giải:
a) Chứng minh ba cạnh của 2 tam giác trên bằng nhau
b) Từ câu a) suy ra 2 cặp góc tương ứng bằng nhau.
Lời giải chi tiết:
a) Xét hai tam giác ABD và ACD có:
AB=AC
AD chung
BD=DC
=>\(\Delta \)ABD = \(\Delta \)ACD (c.c.c)
b) Do \(\Delta \)ABD = \(\Delta \)ACD nên \(\widehat B = \widehat C\)( 2 góc tương ứng)
Cho tam giác MNP có \(\widehat M = \widehat N\). Vẽ tia phân giác PK của tam giác \(MNP(K \in MN)\).
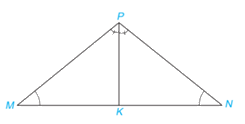
Chứng minh rằng:
a) \(\widehat {MKP} = \widehat {NKP}\);
b) \(\Delta MPK = \Delta NPK\);
c) Tam giác MNP có cân tại \(P\) không?
Phương pháp giải:
a) Sử dụng định lí: Tổng 3 góc trong một tam giác bằng 180 độ
b) Chứng minh 2 tam giác bằng nhau theo trường hợp góc – cạnh - góc
c) Sử dụng định nghĩa tam giác cân: Tam giác MNP cân là tam giác có 2 cạnh bằng nhau
Lời giải chi tiết:
a)
Xét tam giác MPK có:
\(\widehat {PKM} + \widehat {MPK} + \widehat {KMP} = {180^o}\)
Xét tam giác NPK có:
\(\widehat {PKN} + \widehat {NPK} + \widehat {KNP} = {180^o}\)
Mà \(\widehat {KMP} = \widehat {KNP};\,\,\,\widehat {MPK} = \widehat {NPK}\)
Suy ra \(\widehat {MKP} = \widehat {NKP}\).
b)Xét hai tam giác MPK và NPK có:
\(\widehat {MPK} = \widehat {NPK}\)
PK chung
\(\widehat {MKP} = \widehat {NKP}\)
=>\(\Delta MPK = \Delta NPK\)(g.c.g)
c) Do \(\Delta MPK = \Delta NPK\) nên MP=NP (2 cạnh tương ứng)
=> Tam giác MNP cân tại P.
Hãy nêu tên tất cả các tam giác cân trong Hình 4.59. Với mỗi tam cân đó, hãy nêu tên cạnh bên, cạnh đáy, góc ở đỉnh, góc ở đáy của chúng.
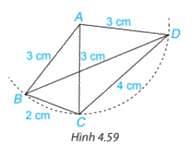
Phương pháp giải:
Tam giác cân là tam giác có hai cạnh bằng nhau. Hai cạnh bằng nhau đó gọi là 2 cạnh bên, cạnh còn lại của tam giác gọi là cạnh đáy.
Lời giải chi tiết:
+) Tam giác ABD cân tại đỉnh A có:
AB, AD là 2 cạnh bên
BD là cạnh đáy
\(\widehat B,\widehat D\) là 2 góc ở đáy
\(\widehat A\) là góc ở đỉnh
+) Tam giác ADC cân tại A có:
AC, AD là 2 cạnh bên
DC là cạnh đáy
\(\widehat C,\widehat D\) là 2 góc ở đáy
\(\widehat A\) là góc ở đỉnh
+) Tam giác ABC cân tại A có:
AB, AC là 2 cạnh bên
BC là cạnh đáy
\(\widehat C,\widehat B\) là 2 góc ở đáy
\(\widehat A\) là góc ở đỉnh
Tính số đo các góc và các cạnh chưa biết của tam giác DEF trong Hình 4.62.
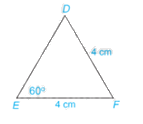
Phương pháp giải:
Chứng minh tam giác DEF cân tại F từ đó suy ra số đo các góc.
Lời giải chi tiết:
Cách 1: Vì tam giác DEF có DF=FE(=4cm) nên tam giác DEF cân tại F.
Mà \(\widehat E=60^0\)
Do đó, \(\Delta DEF \) đều. (Tam giác cân có 1 góc bằng \(60^0\))
\(\Rightarrow \widehat D = \widehat F=\widehat E=60^0\).
Vì tam giác DEF đều nên DE = DF = FE = 4cm.
Cách 2: Xét tam giác DEF có DF=FE(=4cm) nên tam giác DEF cân tại F.
Suy ra \(\widehat E = \widehat D = {60^o}\) ( tính chất tam giác cân)
Áp dụng định lí tổng ba góc trong tam giác vào tam giác DEF, ta có:
\(\begin{array}{l}\widehat D + \widehat E + \widehat F = {180^o}\\ \Rightarrow {60^o} + {60^o} + \widehat F = {180^o}\\ \Rightarrow \widehat F = {60^o}\end{array}\)
Vì tam giác DEF đều nên DE = DF = FE = 4cm.
Hãy nêu tên tất cả các tam giác cân trong Hình 4.59. Với mỗi tam cân đó, hãy nêu tên cạnh bên, cạnh đáy, góc ở đỉnh, góc ở đáy của chúng.
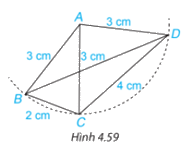
Phương pháp giải:
Tam giác cân là tam giác có hai cạnh bằng nhau. Hai cạnh bằng nhau đó gọi là 2 cạnh bên, cạnh còn lại của tam giác gọi là cạnh đáy.
Lời giải chi tiết:
+) Tam giác ABD cân tại đỉnh A có:
AB, AD là 2 cạnh bên
BD là cạnh đáy
\(\widehat B,\widehat D\) là 2 góc ở đáy
\(\widehat A\) là góc ở đỉnh
+) Tam giác ADC cân tại A có:
AC, AD là 2 cạnh bên
DC là cạnh đáy
\(\widehat C,\widehat D\) là 2 góc ở đáy
\(\widehat A\) là góc ở đỉnh
+) Tam giác ABC cân tại A có:
AB, AC là 2 cạnh bên
BC là cạnh đáy
\(\widehat C,\widehat B\) là 2 góc ở đáy
\(\widehat A\) là góc ở đỉnh
Quan sát tam giác ABC cân tại A như Hình 4.60. Lấy D là trung điểm của đoạn thẳng BC.
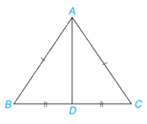
a) Chứng minh rằng \(\Delta \) ABD = \(\Delta \) ACD theo trường hợp cạnh - cạnh - cạnh.
b) Hai góc B và C của tam giác ABC có bằng nhau không?
Phương pháp giải:
a) Chứng minh ba cạnh của 2 tam giác trên bằng nhau
b) Từ câu a) suy ra 2 cặp góc tương ứng bằng nhau.
Lời giải chi tiết:
a) Xét hai tam giác ABD và ACD có:
AB=AC
AD chung
BD=DC
=>\(\Delta \)ABD = \(\Delta \)ACD (c.c.c)
b) Do \(\Delta \)ABD = \(\Delta \)ACD nên \(\widehat B = \widehat C\)( 2 góc tương ứng)
Cho tam giác MNP có \(\widehat M = \widehat N\). Vẽ tia phân giác PK của tam giác \(MNP(K \in MN)\).
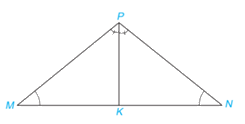
Chứng minh rằng:
a) \(\widehat {MKP} = \widehat {NKP}\);
b) \(\Delta MPK = \Delta NPK\);
c) Tam giác MNP có cân tại \(P\) không?
Phương pháp giải:
a) Sử dụng định lí: Tổng 3 góc trong một tam giác bằng 180 độ
b) Chứng minh 2 tam giác bằng nhau theo trường hợp góc – cạnh - góc
c) Sử dụng định nghĩa tam giác cân: Tam giác MNP cân là tam giác có 2 cạnh bằng nhau
Lời giải chi tiết:
a)
Xét tam giác MPK có:
\(\widehat {PKM} + \widehat {MPK} + \widehat {KMP} = {180^o}\)
Xét tam giác NPK có:
\(\widehat {PKN} + \widehat {NPK} + \widehat {KNP} = {180^o}\)
Mà \(\widehat {KMP} = \widehat {KNP};\,\,\,\widehat {MPK} = \widehat {NPK}\)
Suy ra \(\widehat {MKP} = \widehat {NKP}\).
b)Xét hai tam giác MPK và NPK có:
\(\widehat {MPK} = \widehat {NPK}\)
PK chung
\(\widehat {MKP} = \widehat {NKP}\)
=>\(\Delta MPK = \Delta NPK\)(g.c.g)
c) Do \(\Delta MPK = \Delta NPK\) nên MP=NP (2 cạnh tương ứng)
=> Tam giác MNP cân tại P.
Tính số đo các góc và các cạnh chưa biết của tam giác DEF trong Hình 4.62.
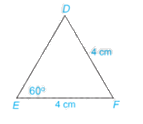
Phương pháp giải:
Chứng minh tam giác DEF cân tại F từ đó suy ra số đo các góc.
Lời giải chi tiết:
Cách 1: Vì tam giác DEF có DF=FE(=4cm) nên tam giác DEF cân tại F.
Mà \(\widehat E=60^0\)
Do đó, \(\Delta DEF \) đều. (Tam giác cân có 1 góc bằng \(60^0\))
\(\Rightarrow \widehat D = \widehat F=\widehat E=60^0\).
Vì tam giác DEF đều nên DE = DF = FE = 4cm.
Cách 2: Xét tam giác DEF có DF=FE(=4cm) nên tam giác DEF cân tại F.
Suy ra \(\widehat E = \widehat D = {60^o}\) ( tính chất tam giác cân)
Áp dụng định lí tổng ba góc trong tam giác vào tam giác DEF, ta có:
\(\begin{array}{l}\widehat D + \widehat E + \widehat F = {180^o}\\ \Rightarrow {60^o} + {60^o} + \widehat F = {180^o}\\ \Rightarrow \widehat F = {60^o}\end{array}\)
Vì tam giác DEF đều nên DE = DF = FE = 4cm.
Thử thách nhỏ
Một tam giác có gì đặc biệt nếu thoả mãn một trong các điều kiện sau:
a) Tam giác có ba góc bằng nhau?
b) Tam giác cân có một góc bằng 60°?
Phương pháp giải:
Áp dụng: Tam giác đều là tam giác có 3 cạnh bằng nhau hoặc ba góc bằng nhau.
Lời giải chi tiết:
a) Tam giác có ba góc bằng nhau là tam giác đều
b) Tam giác cân có 1 góc bằng 60 độ là tam giác đều.
Mục 1 trang 80, 81 SGK Toán 7 tập 1 - Kết nối tri thức thường xoay quanh các bài toán về biểu thức đại số, các phép toán với số hữu tỉ, và ứng dụng của chúng trong thực tế. Để giải quyết các bài toán này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản sau:
Để tính giá trị của một biểu thức đại số, ta thay giá trị của các biến bằng các số cụ thể và thực hiện các phép toán theo đúng thứ tự ưu tiên (ngoặc, nhân chia trước cộng trừ). Ví dụ:
Cho biểu thức A = 2x + 3y với x = 1 và y = -2. Tính giá trị của A.
Giải:
A = 2 * 1 + 3 * (-2) = 2 - 6 = -4
Để viết một biểu thức đại số, ta cần xác định rõ các đại lượng liên quan và mối quan hệ giữa chúng. Ví dụ:
Một người mua x kg táo với giá y đồng một kg. Viết biểu thức biểu thị tổng số tiền người đó phải trả.
Giải:
Biểu thức biểu thị tổng số tiền người đó phải trả là x * y.
Các bài toán ứng dụng thường yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các tình huống thực tế. Để giải quyết các bài toán này, ta cần:
Để đạt kết quả tốt trong quá trình giải bài tập Toán 7, các em cần lưu ý những điều sau:
Hy vọng rằng bài viết này đã cung cấp cho các em những kiến thức và kỹ năng cần thiết để giải quyết các bài tập trong mục 1 trang 80, 81 SGK Toán 7 tập 1 - Kết nối tri thức. Chúc các em học tập tốt và đạt kết quả cao!
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục tri thức. Hãy truy cập website của chúng tôi để khám phá thêm nhiều tài liệu học tập hữu ích khác.