Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 7 tại giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2 trang 37, 38 sách giáo khoa Toán 7 tập 2 chương trình Kết nối tri thức.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong học tập.
Tính (2x – 3) . (x^2 – 5x + 1) bằng cách thực hiện các bước sau: Bước 1: Nhân 2x với đa thức x^2 – 5x + 1 Bước 2: Nhân (-3) với đa thức x^2 – 5x + 1 Bước 3: Cộng các đa thức thu được ở hai bước trên và thu gọn Kết quả thu được là tích của đa thức 2x – 3 với đa thức x^2 – 5x + 1
Tính (2x – 3) . (x2 – 5x + 1) bằng cách thực hiện các bước sau:
Bước 1: Nhân 2x với đa thức x2 – 5x + 1
Bước 2: Nhân (-3) với đa thức x2 – 5x + 1
Bước 3: Cộng các đa thức thu được ở hai bước trên và thu gọn
Kết quả thu được là tích của đa thức 2x – 3 với đa thức x2 – 5x + 1
Phương pháp giải:
Thực hiện theo 3 bước trên
Lời giải chi tiết:
Ta có:
(2x – 3) . (x2 – 5x + 1)
= 2x. (x2 – 5x + 1) + (-3). (x2 – 5x + 1)
= 2x . x2 + 2x . (-5x) + 2x . 1 + (-3).x2 + (-3).(-5x) + (-3). 1
= 2x3 + (-10x2 ) + 2x + (-3x2) + 15x + (-3)
= 2x3 + (-10x2 + -3x2) + (2x + 15x) + (-3)
Rút gọn biểu thức (x – 2) . (2x3 – x2 + 1) + (x – 2) x2(1 – 2x)
Phương pháp giải:
Sử dụng tính chất phân phối của phép nhân đối với phép cộng
Lời giải chi tiết:
(x – 2) . (2x3 – x2 + 1) + (x – 2) x2(1 – 2x)
= (x – 2). [(2x3 – x2 + 1) + x2(1 – 2x)]
= (x – 2). [2x3 – x2 + 1 + x2 . 1 + x2 . (-2x)]
= (x – 2) . (2x3 – x2 + 1 + x2 – 2x3)
= (x – 2) .1
= x – 2
Trở lại bài toán đoán tuổi, để giải thích bí mật trong bài toán đoán tuổi của anh Pi, em hãy thực hiện các yêu cầu sau:
* Gọi x là tuổi cần đoán. Tìm đa thức ( biến x) biểu thị kết quả thứ nhất và kết quả thứ hai
* Tìm đa thức biểu thị kết quả cuối cùng.
Từ đó hãy nêu cách tìm x.
Phương pháp giải:
Tìm đa thức biểu thị từng kết quả thứ nhất và thứ hai.
Lấy kết quả thứ nhất trừ đi kết quả thứ hai.
Lời giải chi tiết:
Đa thức biểu thị kết quả thứ nhất: K = (x + 1)2
Đa thức biểu thị kết quả thứ hai: H = (x – 1)2
Đa thức biểu thị kết quả cuối cùng:
Q = K – H = (x + 1)2 - (x – 1)2
= (x+1).(x+1) - (x – 1). (x – 1)
= x.(x+1) + 1.(x+1) - x(x-1) + (-1). (x-1)
= x.x + x.1 + 1.x + 1.1 –[ x.x – x .1 + (-1).x + (-1) . (-1)]
= x2 + x + x + 1 – (x2 – x – x + 1)
= x2 + x + x + 1 – x2 + x + x – 1
= (x2 - x2 ) + (x+x+x+x) + (1- 1)
= 4x
Để tìm x, ta lấy kết quả cuối cùng chia cho 4
Tính (x3 – 2x2 + x – 1)(3x – 2). Trình bày lời giải theo 2 cách.
Phương pháp giải:
Cách 1: Muốn nhân một đa thức với một đa thức, ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các tích với nhau
Cách 2: Đặt tính nhân:
+ Nhân lần lượt mỗi hạng tử ở dòng dưới với đa thức ở dòng trên và viết kết quả trong một dòng riêng.
+ Viết các dòng sao cho các hạng tử cùng bậc thẳng cột với nhau để thực hiện phép cộng theo cột.
Lời giải chi tiết:
Cách 1:
(x3 – 2x2 + x – 1) (3x – 2)
= x3 . (3x – 2) + (-2x2) .(3x – 2) + x .(3x – 2) + (-1) . (3x – 2)
= x3 . 3x + x3 . (-2) + (-2x2). 3x + (-2x2) . (-2) + x . 3x + x. (-2) + (-1). 3x + (-1). (-2)
= 3x4 – 2x3 – 6x3 + 4x2 + 3x2 – 2x – 3x + 2
= 3x4 + (-2x3 -6x3) + (4x2 + 3x2 ) + (-2x – 3x) + 2
= x4 + (-8x3) + 7x2 + (-5x) + 2
= x4 – 8x3 +7x2 – 5x + 2
Cách 2:
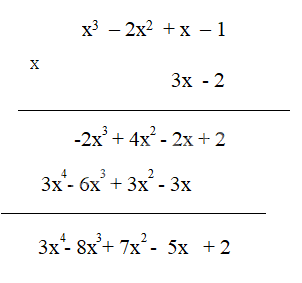
2. Nhân đa thức với đa thức
Tính (2x – 3) . (x2 – 5x + 1) bằng cách thực hiện các bước sau:
Bước 1: Nhân 2x với đa thức x2 – 5x + 1
Bước 2: Nhân (-3) với đa thức x2 – 5x + 1
Bước 3: Cộng các đa thức thu được ở hai bước trên và thu gọn
Kết quả thu được là tích của đa thức 2x – 3 với đa thức x2 – 5x + 1
Phương pháp giải:
Thực hiện theo 3 bước trên
Lời giải chi tiết:
Ta có:
(2x – 3) . (x2 – 5x + 1)
= 2x. (x2 – 5x + 1) + (-3). (x2 – 5x + 1)
= 2x . x2 + 2x . (-5x) + 2x . 1 + (-3).x2 + (-3).(-5x) + (-3). 1
= 2x3 + (-10x2 ) + 2x + (-3x2) + 15x + (-3)
= 2x3 + (-10x2 + -3x2) + (2x + 15x) + (-3)
Tính (x3 – 2x2 + x – 1)(3x – 2). Trình bày lời giải theo 2 cách.
Phương pháp giải:
Cách 1: Muốn nhân một đa thức với một đa thức, ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các tích với nhau
Cách 2: Đặt tính nhân:
+ Nhân lần lượt mỗi hạng tử ở dòng dưới với đa thức ở dòng trên và viết kết quả trong một dòng riêng.
+ Viết các dòng sao cho các hạng tử cùng bậc thẳng cột với nhau để thực hiện phép cộng theo cột.
Lời giải chi tiết:
Cách 1:
(x3 – 2x2 + x – 1) (3x – 2)
= x3 . (3x – 2) + (-2x2) .(3x – 2) + x .(3x – 2) + (-1) . (3x – 2)
= x3 . 3x + x3 . (-2) + (-2x2). 3x + (-2x2) . (-2) + x . 3x + x. (-2) + (-1). 3x + (-1). (-2)
= 3x4 – 2x3 – 6x3 + 4x2 + 3x2 – 2x – 3x + 2
= 3x4 + (-2x3 -6x3) + (4x2 + 3x2 ) + (-2x – 3x) + 2
= x4 + (-8x3) + 7x2 + (-5x) + 2
= x4 – 8x3 +7x2 – 5x + 2
Cách 2:
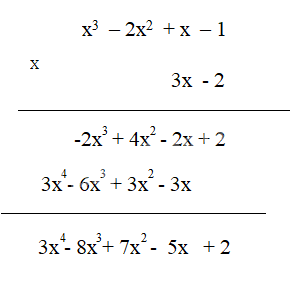
Rút gọn biểu thức (x – 2) . (2x3 – x2 + 1) + (x – 2) x2(1 – 2x)
Phương pháp giải:
Sử dụng tính chất phân phối của phép nhân đối với phép cộng
Lời giải chi tiết:
(x – 2) . (2x3 – x2 + 1) + (x – 2) x2(1 – 2x)
= (x – 2). [(2x3 – x2 + 1) + x2(1 – 2x)]
= (x – 2). [2x3 – x2 + 1 + x2 . 1 + x2 . (-2x)]
= (x – 2) . (2x3 – x2 + 1 + x2 – 2x3)
= (x – 2) .1
= x – 2
Trở lại bài toán đoán tuổi, để giải thích bí mật trong bài toán đoán tuổi của anh Pi, em hãy thực hiện các yêu cầu sau:
* Gọi x là tuổi cần đoán. Tìm đa thức ( biến x) biểu thị kết quả thứ nhất và kết quả thứ hai
* Tìm đa thức biểu thị kết quả cuối cùng.
Từ đó hãy nêu cách tìm x.
Phương pháp giải:
Tìm đa thức biểu thị từng kết quả thứ nhất và thứ hai.
Lấy kết quả thứ nhất trừ đi kết quả thứ hai.
Lời giải chi tiết:
Đa thức biểu thị kết quả thứ nhất: K = (x + 1)2
Đa thức biểu thị kết quả thứ hai: H = (x – 1)2
Đa thức biểu thị kết quả cuối cùng:
Q = K – H = (x + 1)2 - (x – 1)2
= (x+1).(x+1) - (x – 1). (x – 1)
= x.(x+1) + 1.(x+1) - x(x-1) + (-1). (x-1)
= x.x + x.1 + 1.x + 1.1 –[ x.x – x .1 + (-1).x + (-1) . (-1)]
= x2 + x + x + 1 – (x2 – x – x + 1)
= x2 + x + x + 1 – x2 + x + x – 1
= (x2 - x2 ) + (x+x+x+x) + (1- 1)
= 4x
Để tìm x, ta lấy kết quả cuối cùng chia cho 4
Mục 2 của chương trình Toán 7 tập 2 Kết nối tri thức tập trung vào việc ôn tập và củng cố các kiến thức về số hữu tỉ, phép cộng, trừ, nhân, chia số hữu tỉ, và các tính chất của các phép toán này. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các chương trình Toán học ở các lớp trên.
Mục 2 trang 37,38 SGK Toán 7 tập 2 bao gồm các bài tập vận dụng kiến thức đã học để giải quyết các bài toán thực tế. Các bài tập này thường yêu cầu học sinh:
Bài 1 yêu cầu học sinh thực hiện các phép tính cộng, trừ, nhân, chia số hữu tỉ. Để giải bài này, học sinh cần nắm vững các quy tắc về dấu của số hữu tỉ và các phép toán với số hữu tỉ.
Ví dụ:
Tính: a) 1/2 + 3/4; b) -2/3 - 1/6; c) 2/5 * (-3/7); d) -4/9 : 2/3
Lời giải:
Bài 2 yêu cầu học sinh tìm x trong các phương trình có chứa số hữu tỉ. Để giải bài này, học sinh cần sử dụng các quy tắc về chuyển vế và các phép toán với số hữu tỉ.
Ví dụ:
Tìm x: a) x + 1/2 = 3/4; b) x - 2/3 = 1/6; c) 2x = -4/5; d) x : 3/2 = -6/7
Lời giải:
Bài 3 thường là các bài toán ứng dụng thực tế, yêu cầu học sinh sử dụng kiến thức về số hữu tỉ để giải quyết các vấn đề trong cuộc sống.
Ví dụ:
Một người nông dân có 2/5 mảnh đất trồng lúa, 1/3 mảnh đất trồng rau, còn lại là trồng cây ăn quả. Hỏi diện tích đất trồng cây ăn quả chiếm bao nhiêu phần diện tích mảnh đất?
Lời giải:
Diện tích đất trồng cây ăn quả chiếm: 1 - 2/5 - 1/3 = 1 - 6/15 - 5/15 = 4/15 (mảnh đất)
Hy vọng với lời giải chi tiết và hướng dẫn cụ thể trên đây, các em học sinh sẽ tự tin hơn khi giải các bài tập trong mục 2 trang 37,38 SGK Toán 7 tập 2 Kết nối tri thức. Chúc các em học tập tốt!