Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 7 tại giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho mục 2 trang 74, 75 sách giáo khoa Toán 7 tập 2 chương trình Kết nối tri thức.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, tự tin giải các bài tập và đạt kết quả tốt trong môn Toán.
Mỗi tam giác có mấy đường phân giác?
Mỗi tam giác có mấy đường phân giác?
Phương pháp giải:
Trong tam giác ABC, tia phân giác của góc A cắt cạnh BC tại điểm D thì AD là đường phân giác của tam giác ABC.
Lời giải chi tiết:
Từ mỗi đỉnh của tam giác, ta kẻ được 1 đường phân giác của tam giác nên mỗi tam giác có 3 đường phân giác.
Cho tam giác ABC có hai đường phân giác AM, BN cắt nhau tại điểm I. Hỏi CI có là đường phân giác của góc C không?
Phương pháp giải:
Sử dụng định lí về sự đồng quy của ba đường phân giác của tam giác.
Lời giải chi tiết:
Xét tam giác ABC có 2 đường phân giác của tam giác cắt nhau điểm I nên đường phân giác còn lại của tam giác cũng đi qua điểm I ( tính chất đồng quy của 3 đường phân giác)
Vậy CI có là đường phân giác của góc C.
Chứng minh rằng trong tam giác đều, điểm cách đều 3 cạnh của tam giác là trọng tâm của tam giác đó.
Phương pháp giải:
Sử dụng tính chất trong tam giác cân.
Lời giải chi tiết:
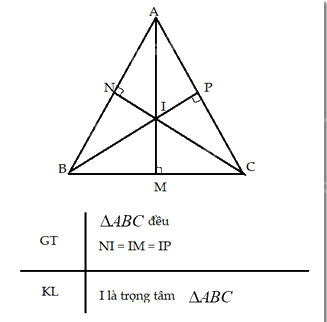
Vì \(\Delta ABC\) đều nên AB = AC = BC (tính chất tam giác đều)
Vì I là điểm cách đều 3 cạnh của tam giác nên là giao điểm của 3 đường phân giác của tam giác ABC
Áp dụng ví dụ 2, ta được, AI là đường trung tuyến của \(\Delta ABC\)
Tương tự, ta cũng được BI, CI là đường trung tuyến của \(\Delta ABC\)
Vậy I là giao điểm của ba đường đường trung tuyến của \(\Delta ABC\) nên I là trọng tâm của \(\Delta ABC\).
Chú ý:
Với tam giác đều, giao điểm của 3 đường trung tuyến cũng là giao điểm của 3 đường phân giác.
Cắt một tam giác bằng giấy. Hãy gấp tam giác vừa cắt để được ba đường phân giác của nó. Mở tờ giấy ra, hãy quan sát và cho biết ba nếp gấp đó có cùng đi qua một điểm không (H.9.33)
Phương pháp giải:
Gấp theo hướng dẫn
Lời giải chi tiết:
Ba nếp gấp đi qua cùng một điểm.
2. Sự đồng quy của ba đường phân giác trong tam giác
Mỗi tam giác có mấy đường phân giác?
Phương pháp giải:
Trong tam giác ABC, tia phân giác của góc A cắt cạnh BC tại điểm D thì AD là đường phân giác của tam giác ABC.
Lời giải chi tiết:
Từ mỗi đỉnh của tam giác, ta kẻ được 1 đường phân giác của tam giác nên mỗi tam giác có 3 đường phân giác.
Cắt một tam giác bằng giấy. Hãy gấp tam giác vừa cắt để được ba đường phân giác của nó. Mở tờ giấy ra, hãy quan sát và cho biết ba nếp gấp đó có cùng đi qua một điểm không (H.9.33)
Phương pháp giải:
Gấp theo hướng dẫn
Lời giải chi tiết:
Ba nếp gấp đi qua cùng một điểm.
Cho tam giác ABC có hai đường phân giác AM, BN cắt nhau tại điểm I. Hỏi CI có là đường phân giác của góc C không?
Phương pháp giải:
Sử dụng định lí về sự đồng quy của ba đường phân giác của tam giác.
Lời giải chi tiết:
Xét tam giác ABC có 2 đường phân giác của tam giác cắt nhau điểm I nên đường phân giác còn lại của tam giác cũng đi qua điểm I ( tính chất đồng quy của 3 đường phân giác)
Vậy CI có là đường phân giác của góc C.
Chứng minh rằng trong tam giác đều, điểm cách đều 3 cạnh của tam giác là trọng tâm của tam giác đó.
Phương pháp giải:
Sử dụng tính chất trong tam giác cân.
Lời giải chi tiết:
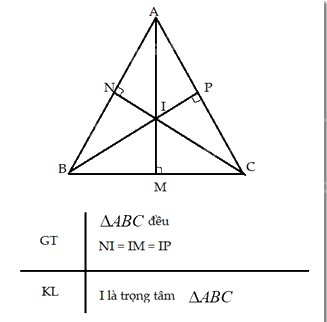
Vì \(\Delta ABC\) đều nên AB = AC = BC (tính chất tam giác đều)
Vì I là điểm cách đều 3 cạnh của tam giác nên là giao điểm của 3 đường phân giác của tam giác ABC
Áp dụng ví dụ 2, ta được, AI là đường trung tuyến của \(\Delta ABC\)
Tương tự, ta cũng được BI, CI là đường trung tuyến của \(\Delta ABC\)
Vậy I là giao điểm của ba đường đường trung tuyến của \(\Delta ABC\) nên I là trọng tâm của \(\Delta ABC\).
Chú ý:
Với tam giác đều, giao điểm của 3 đường trung tuyến cũng là giao điểm của 3 đường phân giác.
Mục 2 trang 74, 75 SGK Toán 7 tập 2 Kết nối tri thức tập trung vào việc ôn tập và củng cố các kiến thức về tam giác cân. Các bài tập trong mục này yêu cầu học sinh vận dụng các định lý, tính chất đã học để giải quyết các bài toán thực tế, rèn luyện kỹ năng tư duy logic và khả năng chứng minh hình học.
Bài 1 yêu cầu học sinh nhắc lại các định nghĩa, tính chất của tam giác cân, tam giác đều. Đồng thời, học sinh cần phân biệt được các loại tam giác khác nhau dựa trên độ dài các cạnh và số đo các góc.
Bài 2 đưa ra các bài toán cụ thể về tam giác cân, yêu cầu học sinh tính toán độ dài các cạnh, số đo các góc, chứng minh các tính chất liên quan. Để giải quyết bài toán này, học sinh cần nắm vững các định lý về tam giác cân, đặc biệt là định lý về góc ở đáy và góc đỉnh.
Bài 3 là một bài tập thực hành, yêu cầu học sinh vẽ hình, viết giả thiết, kết luận và chứng minh các tính chất của tam giác cân. Bài tập này giúp học sinh rèn luyện kỹ năng vẽ hình, trình bày bài toán và chứng minh hình học.
Để giải bài 1, học sinh cần nhớ lại định nghĩa tam giác cân là tam giác có hai cạnh bằng nhau. Tam giác đều là tam giác có ba cạnh bằng nhau. Dựa vào định nghĩa này, học sinh có thể dễ dàng phân biệt các loại tam giác khác nhau.
Để giải bài 2, học sinh cần áp dụng các định lý về tam giác cân. Ví dụ, nếu tam giác ABC cân tại A thì góc B bằng góc C. Ngược lại, nếu góc B bằng góc C thì tam giác ABC cân tại A. Học sinh cần sử dụng các định lý này một cách linh hoạt để giải quyết các bài toán cụ thể.
Để giải bài 3, học sinh cần vẽ hình chính xác, viết giả thiết và kết luận rõ ràng. Sau đó, học sinh cần sử dụng các định lý về tam giác cân để chứng minh các tính chất được yêu cầu. Lưu ý, học sinh cần trình bày bài chứng minh một cách logic và khoa học.
Ngoài sách giáo khoa, học sinh có thể tham khảo thêm các tài liệu sau để học tốt môn Toán 7:
Hy vọng với lời giải chi tiết và hướng dẫn giải bài tập mục 2 trang 74,75 SGK Toán 7 tập 2 Kết nối tri thức, các em học sinh sẽ tự tin hơn trong việc học môn Toán. Chúc các em học tập tốt!