Bài 9.39 trang 84 SGK Toán 7 tập 2 thuộc chương trình Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về ứng dụng tỉ lệ thức vào các bài toán thực tế. Bài tập này thường yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các vấn đề liên quan đến việc chia tỉ lệ.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 9.39 trang 84 SGK Toán 7 tập 2, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
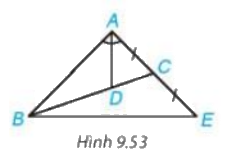
Cho tam giác ABC có đường phân giác AD, D nằm trên BC sao cho BD= 2 DC. Trên đường thẳng AC, lấy điểm E sao cho C là trung điểm của AE (H.9.53). Chứng minh rằng tam giác ABE cân tại A Gợi ý D là trọng tâm của tam gíac ABE, tam giác này có đường phân giác AD đồng thời là trung tuyến.
Đề bài
Cho tam giác ABC có đường phân giác AD, D nằm trên BC sao cho BD= 2 DC. Trên đường thẳng AC, lấy điểm E sao cho C là trung điểm của AE (H.9.53). Chứng minh rằng tam giác ABE cân tại A
Gợi ý D là trọng tâm của tam gíac ABE, tam giác này có đường phân giác AD đồng thời là trung tuyến.
Phương pháp giải - Xem chi tiết
-BD = 2 DC, BC là đường trung tuyến từ đó chứng minh được D là trọng tâm tam giác ABE
-AD là phân giác góc ABE
Lời giải chi tiết
C là trung điểm của AE
\( \Rightarrow \) BC là trung tuyến của tam giác ABE (1)
D thuộc BC, \(BD = 2DC \Rightarrow BD = 2\left( {BC - BD} \right) \Rightarrow 3BD = 2BC \Rightarrow BD = \dfrac{2}{3}BC\)(2)
Từ (1) và (2) suy ra: D là trọng tâm của tam giác ABE
\( \Rightarrow \) AD là đường trung tuyến ứng với BE
Mà AD là đường phân giác của \(\widehat {BAC}\)
\( \Rightarrow \) Tam giác ABE cân tại A.
Bài 9.39 trang 84 SGK Toán 7 tập 2 yêu cầu chúng ta giải quyết một bài toán thực tế liên quan đến việc chia tỉ lệ. Để giải bài này, chúng ta cần nắm vững các khái niệm về tỉ lệ thức và cách áp dụng chúng vào các tình huống cụ thể.
Cho biết ba cạnh của một tam giác có độ dài là 3 cm, 4 cm và 5 cm. Một tam giác khác có ba cạnh tỉ lệ với ba cạnh của tam giác đã cho và có chu vi là 24 cm. Tính độ dài mỗi cạnh của tam giác thứ hai.
Gọi độ dài ba cạnh của tam giác thứ hai lần lượt là a, b, c. Theo đề bài, ta có:
Đặt k là hệ số tỉ lệ, ta có:
Thay vào phương trình a + b + c = 24, ta được:
3k + 4k + 5k = 24
12k = 24
k = 2
Vậy:
Kết luận: Độ dài ba cạnh của tam giác thứ hai lần lượt là 6 cm, 8 cm và 10 cm.
Bài toán này yêu cầu học sinh hiểu rõ mối liên hệ giữa tỉ lệ thức và độ dài các cạnh của tam giác. Việc đặt hệ số tỉ lệ k giúp chúng ta biểu diễn độ dài các cạnh của tam giác thứ hai thông qua độ dài các cạnh của tam giác đã cho. Sau đó, bằng cách sử dụng thông tin về chu vi của tam giác thứ hai, chúng ta có thể tìm ra giá trị của k và tính được độ dài mỗi cạnh.
Bài toán tương tự có thể được mở rộng bằng cách thay đổi độ dài các cạnh của tam giác đã cho hoặc thay đổi chu vi của tam giác thứ hai. Học sinh có thể tự luyện tập thêm các bài toán tương tự để củng cố kiến thức và kỹ năng giải bài tập về tỉ lệ thức.
Hy vọng với lời giải chi tiết này, các em học sinh sẽ hiểu rõ hơn về cách giải bài 9.39 trang 84 SGK Toán 7 tập 2 - Kết nối tri thức. Chúc các em học tập tốt!
| Cạnh tam giác 1 (cm) | Cạnh tam giác 2 (cm) |
|---|---|
| 3 | 6 |
| 4 | 8 |
| 5 | 10 |