Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 7 của giaitoan.edu.vn. Chúng tôi xin giới thiệu lời giải chi tiết các bài tập trang 60, 61, 62 sách giáo khoa Toán 7 tập 1 chương trình Kết nối tri thức.
Mục tiêu của chúng tôi là giúp các em hiểu rõ bản chất bài toán, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
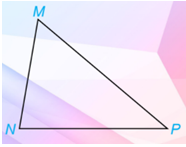
Vẽ tam giác MNP bất kì, đo ba góc của tam giác đó. - Tổng số đo ba góc của tam giác MNP bằng bao nhiêu? - So sánh kết quả của em với các bạn và rút ra nhận xét.
Trở lại tình huống mở đầu, tổng ba góc tại mỗi đỉnh chung của ba tam giác (chẳng hạn tại B trong Hình 4.1) bằng bao nhiêu độ? Ba điểm A, B, C có thẳng hàng không?
Phương pháp giải:
Quan sát điểm B trong hình 4.1 và trả lời câu hỏi
Lời giải chi tiết:
Tổng ba góc tại mỗi đỉnh chung của ba tam giác bằng 180 độ.
Ba điểm A,B,C có thẳng hàng.
Cho tam giác ABC vuông tại A. Tính tổng hai góc B và C.
Phương pháp giải:
Áp dụng định lí: Tổng ba góc của một tam giác bằng 180 độ.
Lời giải chi tiết:
Do tổng ba góc của một tam giác bằng 180 độ nên:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = {180^o}\\{90^o} + \widehat B + \widehat C = {180^o}\\\widehat B + \widehat C = {180^o} - {90^o}\\\widehat B + \widehat C = {90^o}\end{array}\)
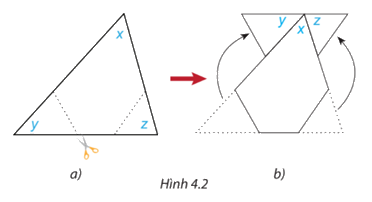
Cắt một hình tam giác bằng giấy bất kì (H.4.2a). Đánh dấu ba góc là x, y, z. Cắt hai góc y, z và ghép lên góc \(x\) như Hình \(4.2\;{\rm{b}}\). Từ đó, em hãy dự đoán tổng số đo các góc x, y, z của tam giác ban đầu.
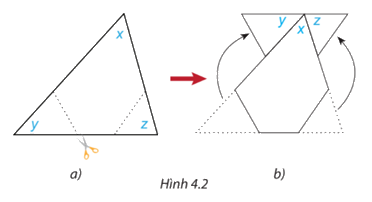
Phương pháp giải:
Quan sát hình 4.2b để trả lời câu hỏi
Lời giải chi tiết:
Tổng số đo các góc x,y,z của tam giác ban đầu bằng số đo của góc bẹt và bằng 180 độ.
Vẽ tam giác MNP bất kì, đo ba góc của tam giác đó.
- Tổng số đo ba góc của tam giác MNP bằng bao nhiêu?
- So sánh kết quả của em với các bạn và rút ra nhận xét.
Phương pháp giải:
Dùng thước đo góc đo ba góc của tam giác MNP rồi trả lời câu hỏi.
Từ đó rút ra nhận xét về tổng ba góc của một tam giác.
Lời giải chi tiết:
Tổng số đo ba góc của tam giác MNP bằng 180 độ.
=> Tổng ba góc của một tam giác bất kì bằng 180 độ.
Cho tam giác ABC và Cx là tia đối của tia CB (H.4.5)
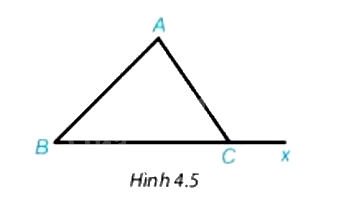
Chứng minh rằng \(\widehat {ACx} = \widehat {BAC} + \widehat {CBA}\)
Phương pháp giải:
Áp dụng định lí: Tổng số đo 3 góc trong 1 tam giác bằng 180 độ.
Số đo góc bẹt bằng 180 độ.
Lời giải chi tiết:
Ta có: \(\widehat {ACB} + \widehat {ACx} = {180^o}\, \Rightarrow \widehat {ACx} = 180 - \widehat {ACB}\)
\(\widehat {BAC} + \widehat {CBA} + \widehat {ACB} = {180^o} \Rightarrow \widehat {BAC} + \widehat {CBA} = {180^o} - \widehat {ACB}\)
Vậy \(\widehat {ACx} = \widehat {BAC} + \widehat {CBA}\)
Video hướng dẫn giải
Vẽ tam giác MNP bất kì, đo ba góc của tam giác đó.
- Tổng số đo ba góc của tam giác MNP bằng bao nhiêu?
- So sánh kết quả của em với các bạn và rút ra nhận xét.
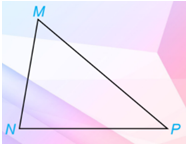
Phương pháp giải:
Dùng thước đo góc đo ba góc của tam giác MNP rồi trả lời câu hỏi.
Từ đó rút ra nhận xét về tổng ba góc của một tam giác.
Lời giải chi tiết:
Tổng số đo ba góc của tam giác MNP bằng 180 độ.
=> Tổng ba góc của một tam giác bất kì bằng 180 độ.
Cắt một hình tam giác bằng giấy bất kì (H.4.2a). Đánh dấu ba góc là x, y, z. Cắt hai góc y, z và ghép lên góc \(x\) như Hình \(4.2\;{\rm{b}}\). Từ đó, em hãy dự đoán tổng số đo các góc x, y, z của tam giác ban đầu.
Phương pháp giải:
Quan sát hình 4.2b để trả lời câu hỏi
Lời giải chi tiết:
Tổng số đo các góc x,y,z của tam giác ban đầu bằng số đo của góc bẹt và bằng 180 độ.
Trở lại tình huống mở đầu, tổng ba góc tại mỗi đỉnh chung của ba tam giác (chẳng hạn tại B trong Hình 4.1) bằng bao nhiêu độ? Ba điểm A, B, C có thẳng hàng không?
Phương pháp giải:
Quan sát điểm B trong hình 4.1 và trả lời câu hỏi
Lời giải chi tiết:
Tổng ba góc tại mỗi đỉnh chung của ba tam giác bằng 180 độ.
Ba điểm A,B,C có thẳng hàng.
Cho tam giác ABC vuông tại A. Tính tổng hai góc B và C.
Phương pháp giải:
Áp dụng định lí: Tổng ba góc của một tam giác bằng 180 độ.
Lời giải chi tiết:
Do tổng ba góc của một tam giác bằng 180 độ nên:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = {180^o}\\{90^o} + \widehat B + \widehat C = {180^o}\\\widehat B + \widehat C = {180^o} - {90^o}\\\widehat B + \widehat C = {90^o}\end{array}\)
Cho tam giác ABC và Cx là tia đối của tia CB (H.4.5)
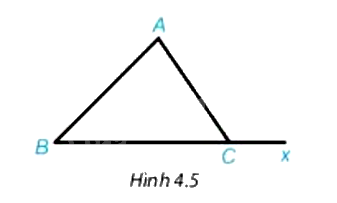
Chứng minh rằng \(\widehat {ACx} = \widehat {BAC} + \widehat {CBA}\)
Phương pháp giải:
Áp dụng định lí: Tổng số đo 3 góc trong 1 tam giác bằng 180 độ.
Số đo góc bẹt bằng 180 độ.
Lời giải chi tiết:
Ta có: \(\widehat {ACB} + \widehat {ACx} = {180^o}\, \Rightarrow \widehat {ACx} = 180 - \widehat {ACB}\)
\(\widehat {BAC} + \widehat {CBA} + \widehat {ACB} = {180^o} \Rightarrow \widehat {BAC} + \widehat {CBA} = {180^o} - \widehat {ACB}\)
Vậy \(\widehat {ACx} = \widehat {BAC} + \widehat {CBA}\)
Chương trình Toán 7 tập 1 Kết nối tri thức tập trung vào việc xây dựng nền tảng vững chắc về các khái niệm toán học cơ bản. Trang 60, 61, 62 của sách giáo khoa chứa đựng những bài tập quan trọng, giúp học sinh củng cố kiến thức về số hữu tỉ, phép cộng, trừ, nhân, chia số hữu tỉ, và các tính chất của chúng.
Các bài tập trên trang 60 thường xoay quanh việc nhận biết, biểu diễn và so sánh các số hữu tỉ. Học sinh cần nắm vững khái niệm số hữu tỉ là gì, cách biểu diễn chúng dưới dạng phân số, và cách so sánh chúng dựa trên mẫu số và tử số.
Trang 61 tập trung vào việc thực hành các phép toán cơ bản với số hữu tỉ. Học sinh cần nắm vững quy tắc cộng, trừ, nhân, chia số hữu tỉ, và áp dụng chúng để giải các bài toán cụ thể.
Trang 62 đi sâu vào việc khám phá các tính chất của phép cộng, trừ, nhân, chia số hữu tỉ, như tính giao hoán, tính kết hợp, tính chất phân phối của phép nhân đối với phép cộng. Việc hiểu rõ các tính chất này giúp học sinh giải toán nhanh chóng và chính xác hơn.
| Tính chất | Ví dụ |
|---|---|
| Tính giao hoán của phép cộng | a + b = b + a |
| Tính kết hợp của phép cộng | (a + b) + c = a + (b + c) |
| Tính chất phân phối của phép nhân đối với phép cộng | a(b + c) = ab + ac |
Lời khuyên khi giải bài tập:
Tầm quan trọng của việc nắm vững kiến thức về số hữu tỉ:
Kiến thức về số hữu tỉ là nền tảng quan trọng cho việc học toán ở các lớp trên. Việc nắm vững kiến thức này giúp học sinh giải quyết các bài toán phức tạp hơn, và ứng dụng toán học vào thực tế một cách hiệu quả.
Giaitoan.edu.vn hy vọng rằng với lời giải chi tiết và những lời khuyên hữu ích trên đây, các em học sinh sẽ tự tin hơn trong việc giải các bài tập Toán 7 trang 60, 61, 62 SGK Kết nối tri thức. Chúc các em học tập tốt!