Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 7 tập 2 của giaitoan.edu.vn. Ở đây, chúng tôi cung cấp lời giải chi tiết và dễ hiểu cho từng bài tập trong SGK Toán 7 tập 2 - Kết nối tri thức, đặc biệt là mục 2 trang 96, 97, 98.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong học tập.
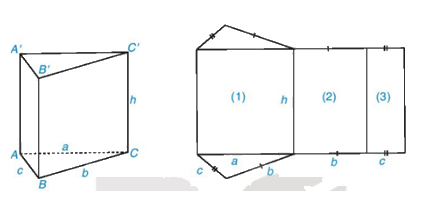
Quan sát hình lăng trụ đứng tam giác ABC. A'B'C' và hình triển khai của nó. Hãy chỉ ra sự tương ứng giữa các mặt bên và các mặt hình chữ nhật của hình khai triển.
Tính tổng diện tích các hình chữ nhật (1), (2), (3) và so sánh với tích của chu vi đáy với chiều cao của hình lăng trụ đứng ở hình trên.
Phương pháp giải:
-Diện tích hình chữ nhật = chiều dài . chiều rộng
-Chu vi tam giác giác = tổng ba cạnh.
Lời giải chi tiết:
Tổng diện tích các hình chữ nhật (1), (2), (3)\( = ha + hb + hc = h\left( {a + b + c} \right)\).
Chu vi đáy của hình lăng trụ \( = a + b + c\)
Tích của chu vi đáy với chiều cao của hình lăng trụ đứng \( = h\left( {a + b + c} \right)\)
\( \Rightarrow \) Tổng diện tích các hình chữ nhật (1), (2), (3) = tích của chu vi đáy với chiều cao của hình lăng trụ đứng
Quan sát hình lăng trụ đứng tam giác ABC. A'B'C' và hình triển khai của nó. Hãy chỉ ra sự tương ứng giữa các mặt bên và các mặt hình chữ nhật của hình khai triển.
Phương pháp giải:
-Cạnh AC = a, BC = b, AB = c
-Tìm hình chữ nhật tương ứng.
Lời giải chi tiết:
Mặt bên tương ứng với hình chữ nhật như sau
(1)-ACC’A’
(2)- BCC’B’
(3)-ABB’A’
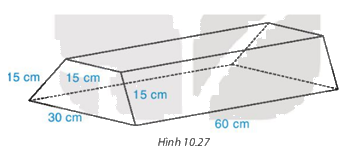
Một khúc gỗ dùng để chặn bánh xe ( giúp xe không bị trôi khi dừng đỗ ) có dạng hình lăng trụ đứng, đáy là hình thang cân có kích thước như hình 10.27. Người ta sơn xung quanh khúc gỗ này ( không sơn hai đầu hình thang cân ). Mỗi mét vuông sơn chi phí hết 20 000 đồng. Hỏi sơn xung quanh như vậy hết bao nhiêu tiền?
Phương pháp giải:
-Tính diện tích xung quanh hình lăng trụ = chu vi đáy x chiều cao
Chu vi đáy hình thang cân = tổng 4 cạnh của hình thang
-Tính tổng chi phí = diện tích xung quanh x 20000đ
Lời giải chi tiết:
Chu vi mặt đáy của hình lăng trụ là:
\(15 + 15 + 15 + 30 = 75 (cm)\)
Diện tích xung quanh khúc gỗ là :
\(75.60 = 4500\left( {c{m^2}} \right) = 0,45\left( {{m^2}} \right)\)
Khi sơn xung quanh, tổng chi phí là :
\(0,45.20000 = 9000\)(đồng)
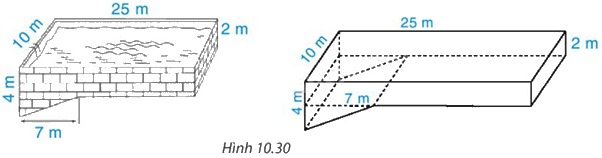
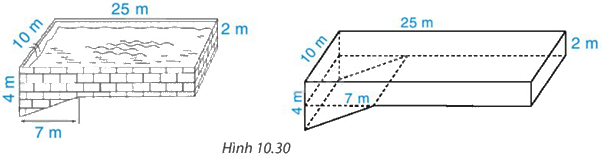
Một bể bơi có hình dạng và kích thước như Hình 10.30. Hình dạng của bể bơi được ghép bởi một hình hộp chữ nhật và một hình lăng trụ đứng tam giác. Khi bể bơi đầy ắp nước thì nó chứa bao nhiêu mét khối nước (bỏ qua độ dày của thành bể).
Phương pháp giải:
Số mét khối nước của bể bơi chính là thể tích của bể bơi.
Bể bơi được tạo bởi một hình hộp chữ nhật và một hình lăng trụ đứng tam giác nên thể tích bể bơi bằng tổng thể tích của hai hình đó.
Thể tích hình hộp chữ nhật là: V = chiều dài.chiều rộng.chiều cao.
Thể tích hình lăng trụ đứng là: V = Sđáy.chiều cao.
Lời giải chi tiết:
Thể tích hình hộp chữ nhật là:
\({V_{hhcn}} = 10.25.2 = 500\left( {{m^3}} \right)\)
Mặt đáy của hình lăng trụ đứng là tam giác vuông có 1 cạnh góc vuông bằng 7m, cạnh góc vuông còn lại là:
4 – 2 = 2 (m)
Thể tích hình lăng trụ đứng là:
\({V_{ltd}} = 10.\left(\frac{1}{2}.7.2\right) = 70\left( {{m^3}} \right)\)
Khi bể bơi đầy ắp nước thì nó chứa số mét khối nước là:
\(V = {V_{hhcn}} + {V_{ltd}} = 500 + 70 = 570\left( {{m^3}} \right)\)
Vậy khi bể bơi đầy ắp nước thì nó chứa 570 mét khối nước.
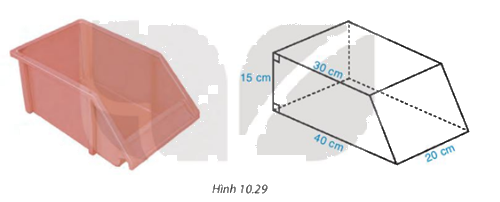
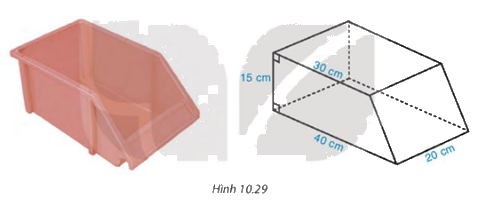
Một chiếc khay đựng linh kiện bằng nhựa, có dạng hình lăng trụ đứng, đáy là hình thang vuông với độ dài hai cạnh đáy là 30 cm, 40 cm và các kích thước như hình 10.29. Tính thể tích của khay.
Phương pháp giải:
Áp dụng công thức:\(V = {S_{day}}.h\)
\({S_{day}} = \dfrac{{\left( {day\,lon + day\,nho} \right)x\,chieu\,cao}}{2}\), h = 20
Lời giải chi tiết:
Diện tích đáy của hình lăng trụ là :
\(\dfrac{{\left( {30 + 40} \right).15}}{2} = 525\left( {c{m^2}} \right)\)
Thể tích của khay là :
\(V = 525.20 = 10500\left( {c{m^3}} \right)\)
Một lều chữ A dạng hình lăng trụ đứng có kích thước như hình 10.26. Tính diện tích vải để làm hai mái và trải đáy của lều.
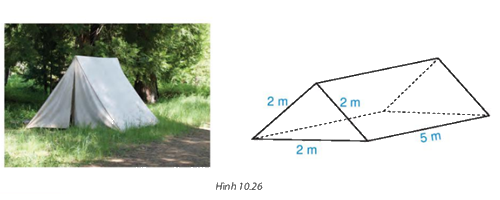
Phương pháp giải:
-Tính diện tích xung quanh hình lăng trụ = chu vi đáy . chiều cao
Lời giải chi tiết:
Diện tích vải để làm hai mái và trải đáy của lều chính là diện tích xung quanh hình lăng trụ:
\(\left( {2 + 2 + 2} \right).5 = 30\left( {{m^2}} \right)\)
Quan sát hình lăng trụ đứng tam giác ABC. A'B'C' và hình triển khai của nó. Hãy chỉ ra sự tương ứng giữa các mặt bên và các mặt hình chữ nhật của hình khai triển.
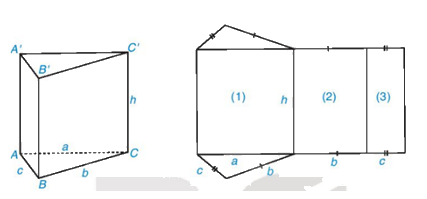
Phương pháp giải:
-Cạnh AC = a, BC = b, AB = c
-Tìm hình chữ nhật tương ứng.
Lời giải chi tiết:
Mặt bên tương ứng với hình chữ nhật như sau
(1)-ACC’A’
(2)- BCC’B’
(3)-ABB’A’
Tính tổng diện tích các hình chữ nhật (1), (2), (3) và so sánh với tích của chu vi đáy với chiều cao của hình lăng trụ đứng ở hình trên.
Phương pháp giải:
-Diện tích hình chữ nhật = chiều dài . chiều rộng
-Chu vi tam giác giác = tổng ba cạnh.
Lời giải chi tiết:
Tổng diện tích các hình chữ nhật (1), (2), (3)\( = ha + hb + hc = h\left( {a + b + c} \right)\).
Chu vi đáy của hình lăng trụ \( = a + b + c\)
Tích của chu vi đáy với chiều cao của hình lăng trụ đứng \( = h\left( {a + b + c} \right)\)
\( \Rightarrow \) Tổng diện tích các hình chữ nhật (1), (2), (3) = tích của chu vi đáy với chiều cao của hình lăng trụ đứng
Một lều chữ A dạng hình lăng trụ đứng có kích thước như hình 10.26. Tính diện tích vải để làm hai mái và trải đáy của lều.
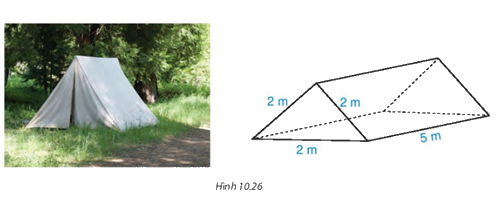
Phương pháp giải:
-Tính diện tích xung quanh hình lăng trụ = chu vi đáy . chiều cao
Lời giải chi tiết:
Diện tích vải để làm hai mái và trải đáy của lều chính là diện tích xung quanh hình lăng trụ:
\(\left( {2 + 2 + 2} \right).5 = 30\left( {{m^2}} \right)\)
Một khúc gỗ dùng để chặn bánh xe ( giúp xe không bị trôi khi dừng đỗ ) có dạng hình lăng trụ đứng, đáy là hình thang cân có kích thước như hình 10.27. Người ta sơn xung quanh khúc gỗ này ( không sơn hai đầu hình thang cân ). Mỗi mét vuông sơn chi phí hết 20 000 đồng. Hỏi sơn xung quanh như vậy hết bao nhiêu tiền?
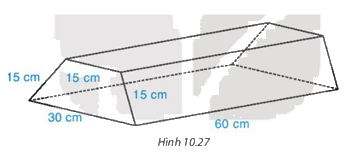
Phương pháp giải:
-Tính diện tích xung quanh hình lăng trụ = chu vi đáy x chiều cao
Chu vi đáy hình thang cân = tổng 4 cạnh của hình thang
-Tính tổng chi phí = diện tích xung quanh x 20000đ
Lời giải chi tiết:
Chu vi mặt đáy của hình lăng trụ là:
\(15 + 15 + 15 + 30 = 75 (cm)\)
Diện tích xung quanh khúc gỗ là :
\(75.60 = 4500\left( {c{m^2}} \right) = 0,45\left( {{m^2}} \right)\)
Khi sơn xung quanh, tổng chi phí là :
\(0,45.20000 = 9000\)(đồng)
Một chiếc khay đựng linh kiện bằng nhựa, có dạng hình lăng trụ đứng, đáy là hình thang vuông với độ dài hai cạnh đáy là 30 cm, 40 cm và các kích thước như hình 10.29. Tính thể tích của khay.
Phương pháp giải:
Áp dụng công thức:\(V = {S_{day}}.h\)
\({S_{day}} = \dfrac{{\left( {day\,lon + day\,nho} \right)x\,chieu\,cao}}{2}\), h = 20
Lời giải chi tiết:
Diện tích đáy của hình lăng trụ là :
\(\dfrac{{\left( {30 + 40} \right).15}}{2} = 525\left( {c{m^2}} \right)\)
Thể tích của khay là :
\(V = 525.20 = 10500\left( {c{m^3}} \right)\)
Một bể bơi có hình dạng và kích thước như Hình 10.30. Hình dạng của bể bơi được ghép bởi một hình hộp chữ nhật và một hình lăng trụ đứng tam giác. Khi bể bơi đầy ắp nước thì nó chứa bao nhiêu mét khối nước (bỏ qua độ dày của thành bể).
Phương pháp giải:
Số mét khối nước của bể bơi chính là thể tích của bể bơi.
Bể bơi được tạo bởi một hình hộp chữ nhật và một hình lăng trụ đứng tam giác nên thể tích bể bơi bằng tổng thể tích của hai hình đó.
Thể tích hình hộp chữ nhật là: V = chiều dài.chiều rộng.chiều cao.
Thể tích hình lăng trụ đứng là: V = Sđáy.chiều cao.
Lời giải chi tiết:
Thể tích hình hộp chữ nhật là:
\({V_{hhcn}} = 10.25.2 = 500\left( {{m^3}} \right)\)
Mặt đáy của hình lăng trụ đứng là tam giác vuông có 1 cạnh góc vuông bằng 7m, cạnh góc vuông còn lại là:
4 – 2 = 2 (m)
Thể tích hình lăng trụ đứng là:
\({V_{ltd}} = 10.\left(\frac{1}{2}.7.2\right) = 70\left( {{m^3}} \right)\)
Khi bể bơi đầy ắp nước thì nó chứa số mét khối nước là:
\(V = {V_{hhcn}} + {V_{ltd}} = 500 + 70 = 570\left( {{m^3}} \right)\)
Vậy khi bể bơi đầy ắp nước thì nó chứa 570 mét khối nước.
Mục 2 trong SGK Toán 7 tập 2 - Kết nối tri thức tập trung vào việc ôn tập và củng cố các kiến thức đã học về tam giác, các trường hợp bằng nhau của tam giác, và các tính chất liên quan đến góc trong tam giác. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các chương tiếp theo.
Bài tập này yêu cầu học sinh nhắc lại các định nghĩa, tính chất cơ bản của tam giác, các loại tam giác (tam giác đều, tam giác cân, tam giác vuông). Đồng thời, học sinh cần vận dụng các kiến thức này để giải các bài tập liên quan đến việc xác định loại tam giác, tính độ dài các cạnh, và tính số đo các góc.
Đây là phần quan trọng nhất của mục 2. Học sinh cần nắm vững ba trường hợp bằng nhau của tam giác: cạnh - cạnh - cạnh (c-c-c), góc - cạnh - góc (g-c-g), và cạnh - góc - cạnh (c-g-c). Việc hiểu rõ các trường hợp này giúp học sinh chứng minh hai tam giác bằng nhau và từ đó suy ra các tính chất liên quan.
Bài tập này giới thiệu về các điểm đồng quy quan trọng của tam giác: trọng tâm, trực tâm, đường trung tuyến, đường cao, đường phân giác. Học sinh cần hiểu rõ định nghĩa, tính chất và cách xác định các điểm này.
Để giải các bài tập trong mục 2 một cách hiệu quả, học sinh cần:
Ví dụ: Cho tam giác ABC có AB = 5cm, AC = 7cm, BC = 9cm. Chứng minh rằng tam giác ABC không phải là tam giác vuông.
Giải:
Ta có: AB2 + AC2 = 52 + 72 = 25 + 49 = 74
BC2 = 92 = 81
Vì AB2 + AC2 ≠ BC2 nên tam giác ABC không phải là tam giác vuông (theo định lý Pytago đảo).
Để củng cố kiến thức và rèn luyện kỹ năng giải toán, học sinh nên làm thêm các bài tập tương tự trong sách bài tập và các đề thi thử. Ngoài ra, có thể tham khảo các tài liệu học tập trực tuyến và các video hướng dẫn giải bài tập trên giaitoan.edu.vn.
Việc nắm vững kiến thức và kỹ năng giải bài tập trong mục 2 là rất quan trọng đối với học sinh lớp 7. Hy vọng với những hướng dẫn chi tiết và ví dụ minh họa trên, các em sẽ tự tin hơn trong việc học tập và giải quyết các bài toán liên quan đến tam giác.