Giaitoan.edu.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 3 trang 35, 36 sách giáo khoa Toán 7 tập 1 chương trình Kết nối tri thức. Bài viết này sẽ giúp các em học sinh nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi cung cấp đáp án đầy đủ, kèm theo các bước giải chi tiết, giúp các em dễ dàng theo dõi và áp dụng vào các bài tập tương tự.
Biểu diễn các số 3 và -2 trên trục số rồi cho biết mỗi điểm ấy nằm cách gốc O bao nhiêu đơn vị....Không vẽ hình, hãy cho biết khoảng cách của mỗi điểm sau đến gốc O: -4; -1; 0; 1; 4
Từ HĐ1 và HĐ2, hãy tìm giá trị tuyệt đối của các số 3; -2; 0; 4 và -4.
Phương pháp giải:
Giá trị tuyệt đối củasố a là khoảng cách của điểm a đến gốc O
Lời giải chi tiết:
Ta có: \(\left| 3 \right| = 3;\left| { - 2} \right| = 2;\left| 0 \right| = 0;\left| 4 \right| = 4;\left| { - 4} \right| = 4\)
Không vẽ hình, hãy cho biết khoảng cách của mỗi điểm sau đến gốc O: -4; -1; 0; 1; 4
Phương pháp giải:
Khoảng cách của 1 số nguyên đến gốc O chính bằng phần số tự nhiên của số nguyên đó.
Lời giải chi tiết:
Khoảng cách của điểm -4 đến gốc O là: 4
Khoảng cách của điểm -1 đến gốc O là: 1
Khoảng cách của điểm 0 đến gốc O là: 0
Khoảng cách của điểm 1 đến gốc O là: 1
Khoảng cách của điểm 4 đến gốc O là: 4
Minh viết: \(\left| { - 2,5} \right| = - 2,5\) đúng hay sai?
Phương pháp giải:
Tính \(\left| { - 2,5} \right|\).
Lời giải chi tiết:
Minh viết \(\left| { - 2,5} \right| = - 2,5\) là sai vì \(\left| { - 2,5} \right| = 2,5\)
Chú ý:
Giá trị tuyệt đối của một số thực luôn không âm
Liệt kê các phần tử của tập hợp \(A = \left\{ {x|x \in \mathbb{Z},\left| x \right| < 5} \right\}\)
Phương pháp giải:
Tìm các số nguyên x có giá trị tuyệt đối nhỏ hơn 5.
Lời giải chi tiết:
Các phần tử của tập hợp A là: 0;1; -1;2; -2 ;3; -3;4; -4.
Tính: a) |-2,3|; b) |\(\dfrac{7}{5}\)|; c) |-11|; d) |\(-\sqrt{8}\)|
Phương pháp giải:
|a| = a nếu \(a \ge 0\)
|a| = -a nếu a < 0
Lời giải chi tiết:
a) |-2,3| = 2,3;
b) |\(\dfrac{7}{5}\)| = \(\dfrac{7}{5}\);
c) |-11| = 11;
d) |\(-\sqrt{8}\)| = \(\sqrt{8}\)
Biểu diễn các số 3 và -2 trên trục số rồi cho biết mỗi điểm ấy nằm cách gốc O bao nhiêu đơn vị.
Phương pháp giải:
Biểu diễn các số 3 và -2 trên trục số và nhận xét
Lời giải chi tiết:
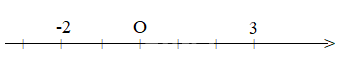
Điểm 3 cách gốc O là 3 đơn vị
Điểm -2 cách gốc O là 2 đơn vị
Biểu diễn các số 3 và -2 trên trục số rồi cho biết mỗi điểm ấy nằm cách gốc O bao nhiêu đơn vị.
Phương pháp giải:
Biểu diễn các số 3 và -2 trên trục số và nhận xét
Lời giải chi tiết:
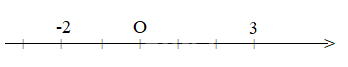
Điểm 3 cách gốc O là 3 đơn vị
Điểm -2 cách gốc O là 2 đơn vị
Không vẽ hình, hãy cho biết khoảng cách của mỗi điểm sau đến gốc O: -4; -1; 0; 1; 4
Phương pháp giải:
Khoảng cách của 1 số nguyên đến gốc O chính bằng phần số tự nhiên của số nguyên đó.
Lời giải chi tiết:
Khoảng cách của điểm -4 đến gốc O là: 4
Khoảng cách của điểm -1 đến gốc O là: 1
Khoảng cách của điểm 0 đến gốc O là: 0
Khoảng cách của điểm 1 đến gốc O là: 1
Khoảng cách của điểm 4 đến gốc O là: 4
Từ HĐ1 và HĐ2, hãy tìm giá trị tuyệt đối của các số 3; -2; 0; 4 và -4.
Phương pháp giải:
Giá trị tuyệt đối củasố a là khoảng cách của điểm a đến gốc O
Lời giải chi tiết:
Ta có: \(\left| 3 \right| = 3;\left| { - 2} \right| = 2;\left| 0 \right| = 0;\left| 4 \right| = 4;\left| { - 4} \right| = 4\)
Minh viết: \(\left| { - 2,5} \right| = - 2,5\) đúng hay sai?
Phương pháp giải:
Tính \(\left| { - 2,5} \right|\).
Lời giải chi tiết:
Minh viết \(\left| { - 2,5} \right| = - 2,5\) là sai vì \(\left| { - 2,5} \right| = 2,5\)
Chú ý:
Giá trị tuyệt đối của một số thực luôn không âm
Tính: a) |-2,3|; b) |\(\dfrac{7}{5}\)|; c) |-11|; d) |\(-\sqrt{8}\)|
Phương pháp giải:
|a| = a nếu \(a \ge 0\)
|a| = -a nếu a < 0
Lời giải chi tiết:
a) |-2,3| = 2,3;
b) |\(\dfrac{7}{5}\)| = \(\dfrac{7}{5}\);
c) |-11| = 11;
d) |\(-\sqrt{8}\)| = \(\sqrt{8}\)
Liệt kê các phần tử của tập hợp \(A = \left\{ {x|x \in \mathbb{Z},\left| x \right| < 5} \right\}\)
Phương pháp giải:
Tìm các số nguyên x có giá trị tuyệt đối nhỏ hơn 5.
Lời giải chi tiết:
Các phần tử của tập hợp A là: 0;1; -1;2; -2 ;3; -3;4; -4.
Mục 3 trong SGK Toán 7 tập 1 Kết nối tri thức tập trung vào việc ôn tập và củng cố các kiến thức về số nguyên, số hữu tỉ, và các phép toán trên chúng. Đây là phần quan trọng để học sinh nắm vững nền tảng toán học, chuẩn bị cho các chương học tiếp theo. Việc giải các bài tập trong mục này không chỉ giúp học sinh hiểu rõ lý thuyết mà còn rèn luyện kỹ năng giải toán, tư duy logic và khả năng áp dụng kiến thức vào thực tế.
Mục 3 bao gồm một loạt các bài tập đa dạng, từ các bài tập cơ bản về tính toán đến các bài tập ứng dụng vào các tình huống thực tế. Các bài tập thường yêu cầu học sinh:
Bài 1 yêu cầu học sinh tính giá trị của các biểu thức chứa các phép toán cộng, trừ, nhân, chia số nguyên và số hữu tỉ. Để giải bài này, học sinh cần nắm vững thứ tự thực hiện các phép toán (nhân, chia trước; cộng, trừ sau) và các quy tắc về dấu của số nguyên và số hữu tỉ.
Ví dụ:
Tính: (-3) + 5 - (-2) * 4
Giải:
Bài 2 yêu cầu học sinh tìm giá trị của x trong các phương trình đơn giản. Để giải bài này, học sinh cần sử dụng các phép toán để biến đổi phương trình về dạng x = một số.
Ví dụ:
Tìm x biết: x + 3 = 7
Giải:
x = 7 - 3
x = 4
Bài 3 yêu cầu học sinh so sánh các số nguyên và số hữu tỉ. Để giải bài này, học sinh cần nắm vững các quy tắc về so sánh số nguyên và số hữu tỉ.
Ví dụ:
So sánh: -2 và 3
Giải:
Vì -2 là số âm và 3 là số dương, nên -2 < 3
Bài 4 thường là các bài toán ứng dụng vào các tình huống thực tế, yêu cầu học sinh sử dụng kiến thức về số nguyên và số hữu tỉ để giải quyết. Các bài toán này giúp học sinh hiểu rõ hơn về ứng dụng của toán học trong cuộc sống.
Ngoài SGK Toán 7 tập 1 Kết nối tri thức, học sinh có thể tham khảo thêm các tài liệu sau:
Việc giải các bài tập trong mục 3 trang 35, 36 SGK Toán 7 tập 1 Kết nối tri thức là một bước quan trọng trong quá trình học tập môn Toán của các em. Hy vọng rằng với lời giải chi tiết và các lưu ý trên, các em sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong môn học này.