Bài 4.24 trang 84 SGK Toán 7 tập 1 thuộc chương trình Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng áp dụng các kiến thức về tam giác cân đã học. Bài tập này thường yêu cầu học sinh chứng minh một tính chất hoặc giải một bài toán liên quan đến tam giác cân.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4.24 trang 84 SGK Toán 7 tập 1, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho tam giác ABC cân tại A và M là trung điểm của đoạn thẳng BC. Chứng minh AM vuông góc với BC và AM là tia phân giác của góc BAC.
Đề bài
Cho tam giác ABC cân tại A và M là trung điểm của đoạn thẳng BC. Chứng minh AM vuông góc với BC và AM là tia phân giác của góc BAC.
Phương pháp giải - Xem chi tiết
Chứng minh 2 tam giác AMC và AMB bằng nhau từ đó suy ra các cặp góc tương ứng bằng nhau.
Lời giải chi tiết
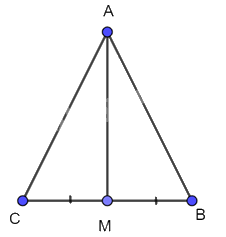
Xét 2 tam giác AMB và AMC có:
AM chung
AB=AC (do tam giác ABC cân tại A)
MB=MC (gt)
\(\Rightarrow\) \(\Delta AMB=\Delta AMC\) (c.c.c)
\(\Rightarrow\) \(\widehat {BAM} = \widehat {CAM}\)(2 góc tương ứng).
Mà tia AM nằm trong góc BAC
\(\Rightarrow\) AM là phân giác của góc BAC
Mặt khác: Do \(\Delta AMB=\Delta AMC\) nên \(\widehat {AMB} = \widehat {AMC}\)(2 góc tương ứng) mà \(\widehat {AMB} + \widehat {AMC} = {180^o}\)( 2 góc kề bù)
Nên: \(\widehat {AMB} = \widehat {AMC} = {90^o}\).
Vậy AM vuông góc với BC.
Bài 4.24 SGK Toán 7 tập 1 - Kết nối tri thức yêu cầu học sinh chứng minh một tính chất liên quan đến tam giác cân. Để giải bài này, chúng ta cần nắm vững các kiến thức cơ bản về tam giác cân, bao gồm định nghĩa, tính chất và các dấu hiệu nhận biết tam giác cân.
Cho tam giác ABC cân tại A. Gọi D là trung điểm của BC. Chứng minh rằng AD là đường phân giác của góc BAC.
Vì tam giác ABC cân tại A, ta có AB = AC. Do D là trung điểm của BC, nên BD = CD.
Xét tam giác ABD và tam giác ACD, ta có:
Do đó, tam giác ABD = tam giác ACD (c-c-c).
Suy ra góc BAD = góc CAD (hai góc tương ứng).
Vậy AD là đường phân giác của góc BAC (đpcm).
Bài giải trên dựa trên việc chứng minh hai tam giác ABD và ACD bằng nhau theo trường hợp cạnh-cạnh-cạnh (c-c-c). Từ đó, suy ra hai góc BAD và CAD bằng nhau, chứng minh AD là đường phân giác của góc BAC.
Ngoài việc chứng minh AD là đường phân giác, chúng ta còn có thể chứng minh AD là đường cao và đường trung tuyến của tam giác ABC. Điều này là do tam giác ABC cân tại A, nên đường trung tuyến xuất phát từ đỉnh A đồng thời là đường cao và đường phân giác.
Tam giác cân xuất hiện rất nhiều trong thực tế, ví dụ như hình dạng của một số loại mái nhà, cầu, hoặc các vật dụng trang trí. Việc hiểu rõ về tam giác cân giúp chúng ta ứng dụng kiến thức toán học vào giải quyết các vấn đề thực tế.
Bài 4.24 trang 84 SGK Toán 7 tập 1 - Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về tam giác cân. Hy vọng với lời giải chi tiết và hướng dẫn trên, các em học sinh sẽ tự tin giải bài tập này và các bài tập tương tự.
| Khái niệm | Định nghĩa |
|---|---|
| Tam giác cân | Tam giác có hai cạnh bằng nhau. |
| Đường phân giác | Đường thẳng chia một góc của tam giác thành hai góc bằng nhau. |
| Đường trung tuyến | Đường thẳng nối một đỉnh của tam giác với trung điểm của cạnh đối diện. |
| Đường cao | Đường thẳng vuông góc với một cạnh của tam giác và đi qua đỉnh đối diện. |