Bài 4.23 trang 84 SGK Toán 7 tập 1 thuộc chương trình Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng áp dụng các kiến thức về tam giác cân đã học. Bài tập này thường yêu cầu học sinh chứng minh một tính chất hoặc giải một bài toán thực tế liên quan đến tam giác cân.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4.23 trang 84 SGK Toán 7 tập 1, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho tam giác ABC cân tại A và các điểm E, F lần lượt nằm trên các cạnh AC, AB sao cho BE vuông góc với AC, CF vuông góc với AB (H.4.69). Chứng minh rằng BE = CF.
Đề bài
Cho tam giác ABC cân tại A và các điểm E, F lần lượt nằm trên các cạnh AC, AB sao cho BE vuông góc với AC, CF vuông góc với AB (H.4.69). Chứng minh rằng BE = CF.
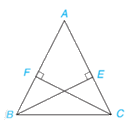
Phương pháp giải - Xem chi tiết
Chứng minh 2 tam giác bằng nhau để suy ra 2 cạnh tương ứng bằng nhau.
Lời giải chi tiết
Do tam giác ABC cân tại A nên: \(\widehat {ABC} = \widehat {ACB}\)(tính chất tam giác cân)
Xét 2 tam giác vuông BFC và CEB:
\(\widehat {ABC} = \widehat {ACB}\)
BC chung
=>\(\Delta BFC = \Delta CEB\)(cạnh huyền – góc nhọn)
=>\(CF=BE\) (2 cạnh tương ứng).
Bài 4.23 trang 84 SGK Toán 7 tập 1 - Kết nối tri thức yêu cầu học sinh giải một bài toán liên quan đến tam giác cân. Để giải bài toán này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về tam giác cân, bao gồm:
Nội dung bài toán: (Giả sử bài toán là: Cho tam giác ABC cân tại A. Gọi D là trung điểm của BC. Chứng minh AD là đường phân giác của góc BAC.)
a) Chứng minh AD là đường phân giác của góc BAC:
Vì tam giác ABC cân tại A (giả thiết) nên AB = AC (định nghĩa tam giác cân).
Xét tam giác ABD và tam giác ACD, ta có:
Do đó, tam giác ABD = tam giác ACD (cạnh - cạnh - cạnh).
Suy ra ∠BAD = ∠CAD (hai góc tương ứng).
Vậy AD là đường phân giác của góc BAC.
Bài toán này có thể được mở rộng bằng cách thay đổi giả thiết hoặc yêu cầu chứng minh các tính chất khác của tam giác cân. Ví dụ:
Để giải các bài tập tương tự, học sinh cần:
Ví dụ bài tập tương tự:
Cho tam giác MNP cân tại M. Biết ∠N = 40°. Tính ∠P.
Lời giải:
Vì tam giác MNP cân tại M nên ∠N = ∠P (tính chất tam giác cân).
Vậy ∠P = 40°.
Bài 4.23 trang 84 SGK Toán 7 tập 1 - Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về tam giác cân. Hy vọng với lời giải chi tiết và hướng dẫn giải bài tập tương tự, các em học sinh sẽ tự tin hơn trong việc học toán.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Chúc các em học tập tốt!