Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 7. Trong bài viết này, chúng tôi sẽ cùng bạn giải quyết mục 2 trang 8 SGK Toán 7 tập 1 - Kết nối tri thức. Mục tiêu của chúng tôi là giúp bạn nắm vững kiến thức và tự tin giải các bài tập Toán học.
Viết các số hữu tỉ dưới dạng phân số rồi so sánh:...Biểu diễn hai số hữu tỉ -1,5 và ....Sắp xếp các số hữu tỉ sau theo thứ tự từ bé đến lớn...Em hãy giải bài toán mở đầu.
Viết các số hữu tỉ dưới dạng phân số rồi so sánh:
a) -1,5 và \(\frac{5}{2}\); b) -0,375 và \( - \frac{5}{8}\)
Phương pháp giải:
Viết các số hữu tỉ dưới dạng phân số
So sánh 2 phân số.
Số hữu tỉ dương luôn lớn hơn số hữu tỉ âm.
Lời giải chi tiết:
a) Ta có: \( - 1,5 = \frac{{ - 15}}{{10}} = \frac{{ - 3}}{2}\)
Vì -3 < 5 nên \(\frac{{ - 3}}{2} < \frac{5}{2}\)hay -1,5 < \(\frac{5}{2}\)
b) Ta có: \( - 0,375 = \frac{{ - 375}}{{1000}} = \frac{{ - 3}}{8}\)
Vì 3 < 5 nên -3 > -5, do đó \(\frac{{ - 3}}{8} > \frac{{ - 5}}{8}\)
Vậy -0,375 > \( - \frac{5}{8}\)
Sắp xếp các số hữu tỉ sau theo thứ tự từ bé đến lớn.
\(5\frac{1}{4}; - 2;3,125; - \frac{3}{2}.\)
Phương pháp giải:
Số hữu tỉ dương luôn lớn hơn số hữu tỉ âm.
Cách 1:+) Bước 1: Viết các số hữu tỉ dưới dạng phân số.
+) Bước 2: Quy đồng mẫu số các phân số
+) Bước 3: Sắp xếp các số hữu tỉ theo thứ tự từ bé đến lớn.
Cách 2: +) Bước 1: Đưa các số hữu tỉ về dạng số thập phân.
+) Bước 2: So sánh các số thập phân
+) Bước 3: Sắp xếp các số hữu tỉ theo thứ tự từ bé đến lớn
Lời giải chi tiết:
Cách 1: Ta có:
\(\begin{array}{l}5\frac{1}{4} = \frac{{5.4 + 1}}{4} = \frac{{21}}{4} = \frac{{42}}{8}\\ - 2 = \frac{{ - 16}}{8}\\3,125 = \frac{{3125}}{{1000}} = \frac{{25}}{8}\\ - \frac{3}{2} = \frac{{ - 12}}{8}\end{array}\)
Vì -16 < -12 < 25 < 42 nên \(\frac{{ - 16}}{8} < \frac{{ - 12}}{8} < \frac{{25}}{8} < \frac{{42}}{8}\) hay -2 < \(\frac{{ - 3}}{2}\) < 3,125 < \(5\frac{1}{4}\)
Vậy các số hữu tỉ trên sắp xếp theo thứ tự từ bé đến lớn là: -2; \(\frac{{ - 3}}{2}\); 3,125; \(5\frac{1}{4}\)
Cách 2: Ta có: \(5\frac{1}{4}\)= 5,25
\(\frac{{ - 3}}{2}\)= -1,5
Vì -2 < -1,5 < 0 < 3,125 < 5,25 nên -2 < \(\frac{{ - 3}}{2}\) < 3,125 < \(5\frac{1}{4}\)
Vậy các số hữu tỉ trên sắp xếp theo thứ tự từ bé đến lớn là: -2; \(\frac{{ - 3}}{2}\); 3,125; \(5\frac{1}{4}\)
Em hãy giải bài toán mở đầu.
Chỉ số WHtR (Waist to Height Ratio) của một người trưởng thành, được tính bằng tỉ số giữa số đo vòng bụng và số đo chiều cao (cùng một đơn vị đo). Chỉ số này được coi là một công cụ đo lường sức khỏe hữu ích vì có thể dự báo được nguy cơ béo phì, mắc bệnh tim mạch,… Bảng bên cho biết nguy cơ thừa cân, bép phì của một người đàn ông trưởng thành dựa vào chỉ số WHtR.
(Theo hospitamedia.com)
Ông An cao 180 cm, vòng bụng 108 cm.
Ông Chung cao 160 cm, vòng bụng 70 cm.
Theo em, nếu tính theo chỉ số WHtR, sức khỏe của ông An hay ông Chung tốt hơn?
Phương pháp giải:
Tính chỉ số WHtR của mỗi ông:
Chỉ số WHtR = Số đo vòng bụng : Chiều cao
Đối chiếu số liệu vừa tính được với bảng trên.
Lời giải chi tiết:
Chỉ số WHtR của ông An là: \(\frac{{108}}{{180}} = 0,6\)
Chỉ số WHtR của ông Chung là: \(\frac{{70}}{{160}} = 0,4375\)
Ta thấy: Chỉ số WHtR của ông An lớn hơn 0,57 và nhỏ hơn 0,63 nên ông An thừa cân.
Chỉ số WHtR của ông Chung lớn hơn 0,42 và nhỏ hơn hoặc bằng 0,52 nên ông Chung có chỉ số tốt.
Vậy nếu tính theo chỉ số WHtR, sức khỏe của ông Chung tốt hơn.
Biểu diễn hai số hữu tỉ -1,5 và \(\frac{5}{2}\) trên trục số. Em hãy cho biết điểm -1,5 nằm trước hay nằm sau điểm \(\frac{5}{2}\) trên trục số.
Phương pháp giải:
Vẽ trục số, chia đoạn thẳng đơn vị thành 2 phần bằng nhau. Lấy một đoạn làm đơn vị mới ( đơn vị mới bằng \(\frac{1}{2}\) đơn vị cũ)
Quan sát vị trí của 2 điểm vừa biểu diễn
Lời giải chi tiết:
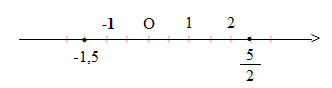
Điểm -1,5 nằm trước điểm \(\frac{5}{2}\) trên trục số.
Chú ý: Nhận xét: Trên trục số nằm ngang, điểm biểu diễn số hữu tỉ nhỏ hơn nằm trước điểm biểu diễn số hữu tỉ lớn hơn.
Viết các số hữu tỉ dưới dạng phân số rồi so sánh:
a) -1,5 và \(\frac{5}{2}\); b) -0,375 và \( - \frac{5}{8}\)
Phương pháp giải:
Viết các số hữu tỉ dưới dạng phân số
So sánh 2 phân số.
Số hữu tỉ dương luôn lớn hơn số hữu tỉ âm.
Lời giải chi tiết:
a) Ta có: \( - 1,5 = \frac{{ - 15}}{{10}} = \frac{{ - 3}}{2}\)
Vì -3 < 5 nên \(\frac{{ - 3}}{2} < \frac{5}{2}\)hay -1,5 < \(\frac{5}{2}\)
b) Ta có: \( - 0,375 = \frac{{ - 375}}{{1000}} = \frac{{ - 3}}{8}\)
Vì 3 < 5 nên -3 > -5, do đó \(\frac{{ - 3}}{8} > \frac{{ - 5}}{8}\)
Vậy -0,375 > \( - \frac{5}{8}\)
Biểu diễn hai số hữu tỉ -1,5 và \(\frac{5}{2}\) trên trục số. Em hãy cho biết điểm -1,5 nằm trước hay nằm sau điểm \(\frac{5}{2}\) trên trục số.
Phương pháp giải:
Vẽ trục số, chia đoạn thẳng đơn vị thành 2 phần bằng nhau. Lấy một đoạn làm đơn vị mới ( đơn vị mới bằng \(\frac{1}{2}\) đơn vị cũ)
Quan sát vị trí của 2 điểm vừa biểu diễn
Lời giải chi tiết:
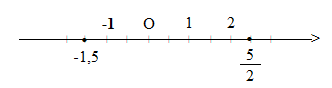
Điểm -1,5 nằm trước điểm \(\frac{5}{2}\) trên trục số.
Chú ý: Nhận xét: Trên trục số nằm ngang, điểm biểu diễn số hữu tỉ nhỏ hơn nằm trước điểm biểu diễn số hữu tỉ lớn hơn.
Sắp xếp các số hữu tỉ sau theo thứ tự từ bé đến lớn.
\(5\frac{1}{4}; - 2;3,125; - \frac{3}{2}.\)
Phương pháp giải:
Số hữu tỉ dương luôn lớn hơn số hữu tỉ âm.
Cách 1:+) Bước 1: Viết các số hữu tỉ dưới dạng phân số.
+) Bước 2: Quy đồng mẫu số các phân số
+) Bước 3: Sắp xếp các số hữu tỉ theo thứ tự từ bé đến lớn.
Cách 2: +) Bước 1: Đưa các số hữu tỉ về dạng số thập phân.
+) Bước 2: So sánh các số thập phân
+) Bước 3: Sắp xếp các số hữu tỉ theo thứ tự từ bé đến lớn
Lời giải chi tiết:
Cách 1: Ta có:
\(\begin{array}{l}5\frac{1}{4} = \frac{{5.4 + 1}}{4} = \frac{{21}}{4} = \frac{{42}}{8}\\ - 2 = \frac{{ - 16}}{8}\\3,125 = \frac{{3125}}{{1000}} = \frac{{25}}{8}\\ - \frac{3}{2} = \frac{{ - 12}}{8}\end{array}\)
Vì -16 < -12 < 25 < 42 nên \(\frac{{ - 16}}{8} < \frac{{ - 12}}{8} < \frac{{25}}{8} < \frac{{42}}{8}\) hay -2 < \(\frac{{ - 3}}{2}\) < 3,125 < \(5\frac{1}{4}\)
Vậy các số hữu tỉ trên sắp xếp theo thứ tự từ bé đến lớn là: -2; \(\frac{{ - 3}}{2}\); 3,125; \(5\frac{1}{4}\)
Cách 2: Ta có: \(5\frac{1}{4}\)= 5,25
\(\frac{{ - 3}}{2}\)= -1,5
Vì -2 < -1,5 < 0 < 3,125 < 5,25 nên -2 < \(\frac{{ - 3}}{2}\) < 3,125 < \(5\frac{1}{4}\)
Vậy các số hữu tỉ trên sắp xếp theo thứ tự từ bé đến lớn là: -2; \(\frac{{ - 3}}{2}\); 3,125; \(5\frac{1}{4}\)
Em hãy giải bài toán mở đầu.
Chỉ số WHtR (Waist to Height Ratio) của một người trưởng thành, được tính bằng tỉ số giữa số đo vòng bụng và số đo chiều cao (cùng một đơn vị đo). Chỉ số này được coi là một công cụ đo lường sức khỏe hữu ích vì có thể dự báo được nguy cơ béo phì, mắc bệnh tim mạch,… Bảng bên cho biết nguy cơ thừa cân, bép phì của một người đàn ông trưởng thành dựa vào chỉ số WHtR.
(Theo hospitamedia.com)
Ông An cao 180 cm, vòng bụng 108 cm.
Ông Chung cao 160 cm, vòng bụng 70 cm.
Theo em, nếu tính theo chỉ số WHtR, sức khỏe của ông An hay ông Chung tốt hơn?
Phương pháp giải:
Tính chỉ số WHtR của mỗi ông:
Chỉ số WHtR = Số đo vòng bụng : Chiều cao
Đối chiếu số liệu vừa tính được với bảng trên.
Lời giải chi tiết:
Chỉ số WHtR của ông An là: \(\frac{{108}}{{180}} = 0,6\)
Chỉ số WHtR của ông Chung là: \(\frac{{70}}{{160}} = 0,4375\)
Ta thấy: Chỉ số WHtR của ông An lớn hơn 0,57 và nhỏ hơn 0,63 nên ông An thừa cân.
Chỉ số WHtR của ông Chung lớn hơn 0,42 và nhỏ hơn hoặc bằng 0,52 nên ông Chung có chỉ số tốt.
Vậy nếu tính theo chỉ số WHtR, sức khỏe của ông Chung tốt hơn.
Mục 2 trang 8 SGK Toán 7 tập 1 - Kết nối tri thức tập trung vào việc ôn tập và củng cố các kiến thức về số tự nhiên, số nguyên, phép toán trên số tự nhiên và số nguyên, cũng như các tính chất cơ bản của chúng. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các chương tiếp theo của môn Toán 7.
Mục 2 trang 8 bao gồm các bài tập vận dụng các kiến thức đã học để giải quyết các bài toán thực tế. Các bài tập thường yêu cầu học sinh:
Bài 1 yêu cầu học sinh thực hiện các phép tính cộng, trừ, nhân, chia số tự nhiên và số nguyên. Để giải bài tập này, học sinh cần nắm vững các quy tắc thực hiện các phép tính trên số tự nhiên và số nguyên.
Ví dụ:
a) 12 + 5 = 17
b) 20 - 8 = 12
c) 3 x 4 = 12
d) 15 : 3 = 5
Bài 2 yêu cầu học sinh tìm giá trị của x trong các phương trình đơn giản. Để giải bài tập này, học sinh cần sử dụng các phép biến đổi tương đương để đưa phương trình về dạng x = một số.
Ví dụ:
a) x + 5 = 10 => x = 10 - 5 = 5
b) x - 3 = 7 => x = 7 + 3 = 10
Bài 3 yêu cầu học sinh điền vào chỗ trống để hoàn thiện các câu phát biểu về các tính chất của phép cộng, phép nhân. Để giải bài tập này, học sinh cần nắm vững các tính chất của phép cộng, phép nhân.
Ví dụ:
a) a + b = b + ... (Tính chất giao hoán của phép cộng)
b) a x b = b x ... (Tính chất giao hoán của phép nhân)
Việc giải bài tập là một phần quan trọng trong quá trình học Toán. Nó giúp học sinh:
Hy vọng rằng với hướng dẫn chi tiết này, bạn đã có thể tự tin giải các bài tập trong Mục 2 trang 8 SGK Toán 7 tập 1 - Kết nối tri thức. Chúc bạn học tốt và đạt kết quả cao trong môn Toán!