Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 7 của giaitoan.edu.vn. Trong bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho mục 1 trang 29, 30 sách giáo khoa Toán 7 tập 1 chương trình Kết nối tri thức.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải bài tập và tự tin hơn trong học tập.
Cắt một hình vuông cạnh bằng 2 dm, rồi cắt nó thành bốn tam giác vuông bằng nhau dọc theo hai đường chéo của hình vuông (H.2.2.a)...Lấy hai trong bốn tam giác nhận được ở trên ghép thành một hình vuông (H.2.2.b). Em hãy tính diện tích hình vuông nhận được.
Người xưa đã tính đường kính thân cây theo quy tắc “quân bát, phát tam, tổn ngũ, quân nhị”, tức là lấy chu vi thân cây chia làm 8 phần bằng nhau (quân bát); bớt đi ba phần (phát tam) còn lại 5 phần (tổn ngũ) rồi chia đôi kết quả (quân nhị). Hãy cho biết người xưa đã ước lượng số \(\pi \) bằng bao nhiêu?
Phương pháp giải:
Từ công thức tính chu vi đường tròn: C = \(\pi \). d \(a = \sqrt S \)\( \Rightarrow d = \frac{C}{\pi }\)\(\)
Thực hiện theo quy tắc “quân bát, phát tam, tổn ngũ, quân nhị”
Lời giải chi tiết:
Theo quy tắc “quân bát, phát tam, tổn ngũ, quân nhị”, có: \(d = \frac{C}{8}.5:2 = \frac{C}{8}.5.\frac{1}{2} = \frac{{5C}}{{16}} = \frac{C}{{\frac{{16}}{5}}}\)
Theo công thức, có: \(d = \frac{C}{\pi }\)
Như vậy, người xưa đã ước lượng số \(\pi \) bằng \(\frac{{16}}{5} = 3,2\).
Dùng thước có vạch chia để đo độ dài cạnh hình vuông nhận được trong HĐ2. Độ dài cạnh hình vuông này bằng bao nhiêu đềximét ?
Phương pháp giải:
Bước 1: Dùng thước đo cạnh hình vuông nhận được trong HĐ2, ta được số liệu có đơn vị cm.
Bước 2: Đổi đơn vị cm sang dm.
Lời giải chi tiết:
Dùng thước đo ta được cạnh hình vuông dài khoảng 14 cm.
Ta có: 14 cm = 1,4 dm
Cắt một hình vuông cạnh bằng 2 dm, rồi cắt nó thành bốn tam giác vuông bằng nhau dọc theo hai đường chéo của hình vuông (H.2.2.a)
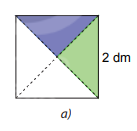
Phương pháp giải:
Cắt theo mô tả của đề bài
Lời giải chi tiết:
Bước 1: Cắt một hình vuông cạnh bằng 2 dm
Bước 2: Cắt hình vuông thành bốn tam giác vuông bằng nhau dọc theo hai đường chéo của hình vuông.
Lấy hai trong bốn tam giác nhận được ở trên ghép thành một hình vuông (H.2.2.b). Em hãy tính diện tích hình vuông nhận được.
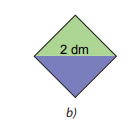
Phương pháp giải:
Ghép 2 tam giác như hình.
Diện tích hình vuông = Diện tích hình vuông ban đầu (cạnh 2 dm) : 2
Lời giải chi tiết:
Lấy hai trong bốn tam giác nhận được ở trên ghép thành một hình vuông.
Vì 2 tam giác vuông chiếm một nửa hình vuông ban đầu nên
Diện tích hình vuông thu được là:
2.2:2= 2 (dm2)
Cắt một hình vuông cạnh bằng 2 dm, rồi cắt nó thành bốn tam giác vuông bằng nhau dọc theo hai đường chéo của hình vuông (H.2.2.a)
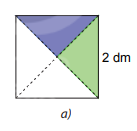
Phương pháp giải:
Cắt theo mô tả của đề bài
Lời giải chi tiết:
Bước 1: Cắt một hình vuông cạnh bằng 2 dm
Bước 2: Cắt hình vuông thành bốn tam giác vuông bằng nhau dọc theo hai đường chéo của hình vuông.
Lấy hai trong bốn tam giác nhận được ở trên ghép thành một hình vuông (H.2.2.b). Em hãy tính diện tích hình vuông nhận được.
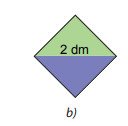
Phương pháp giải:
Ghép 2 tam giác như hình.
Diện tích hình vuông = Diện tích hình vuông ban đầu (cạnh 2 dm) : 2
Lời giải chi tiết:
Lấy hai trong bốn tam giác nhận được ở trên ghép thành một hình vuông.
Vì 2 tam giác vuông chiếm một nửa hình vuông ban đầu nên
Diện tích hình vuông thu được là:
2.2:2= 2 (dm2)
Dùng thước có vạch chia để đo độ dài cạnh hình vuông nhận được trong HĐ2. Độ dài cạnh hình vuông này bằng bao nhiêu đềximét ?
Phương pháp giải:
Bước 1: Dùng thước đo cạnh hình vuông nhận được trong HĐ2, ta được số liệu có đơn vị cm.
Bước 2: Đổi đơn vị cm sang dm.
Lời giải chi tiết:
Dùng thước đo ta được cạnh hình vuông dài khoảng 14 cm.
Ta có: 14 cm = 1,4 dm
Người xưa đã tính đường kính thân cây theo quy tắc “quân bát, phát tam, tổn ngũ, quân nhị”, tức là lấy chu vi thân cây chia làm 8 phần bằng nhau (quân bát); bớt đi ba phần (phát tam) còn lại 5 phần (tổn ngũ) rồi chia đôi kết quả (quân nhị). Hãy cho biết người xưa đã ước lượng số \(\pi \) bằng bao nhiêu?
Phương pháp giải:
Từ công thức tính chu vi đường tròn: C = \(\pi \). d \(a = \sqrt S \)\( \Rightarrow d = \frac{C}{\pi }\)\(\)
Thực hiện theo quy tắc “quân bát, phát tam, tổn ngũ, quân nhị”
Lời giải chi tiết:
Theo quy tắc “quân bát, phát tam, tổn ngũ, quân nhị”, có: \(d = \frac{C}{8}.5:2 = \frac{C}{8}.5.\frac{1}{2} = \frac{{5C}}{{16}} = \frac{C}{{\frac{{16}}{5}}}\)
Theo công thức, có: \(d = \frac{C}{\pi }\)
Như vậy, người xưa đã ước lượng số \(\pi \) bằng \(\frac{{16}}{5} = 3,2\).
Mục 1 trang 29, 30 SGK Toán 7 tập 1 - Kết nối tri thức tập trung vào việc ôn tập và củng cố các kiến thức cơ bản về số hữu tỉ, phép cộng, trừ, nhân, chia số hữu tỉ. Các bài tập trong mục này giúp học sinh rèn luyện kỹ năng thực hiện các phép toán với số hữu tỉ, so sánh số hữu tỉ và áp dụng các tính chất của phép toán để giải quyết các bài toán thực tế.
Bài 1 yêu cầu học sinh điền vào chỗ trống các số hữu tỉ thích hợp để hoàn thiện các câu phát biểu về số hữu tỉ. Bài tập này giúp học sinh ôn lại khái niệm số hữu tỉ, cách biểu diễn số hữu tỉ và các tính chất cơ bản của số hữu tỉ.
Bài 2 yêu cầu học sinh thực hiện các phép cộng, trừ, nhân, chia số hữu tỉ. Bài tập này giúp học sinh rèn luyện kỹ năng thực hiện các phép toán với số hữu tỉ, áp dụng các quy tắc dấu và các tính chất của phép toán.
Bài 3 yêu cầu học sinh so sánh các số hữu tỉ. Bài tập này giúp học sinh rèn luyện kỹ năng so sánh số hữu tỉ, sử dụng các phương pháp so sánh khác nhau như quy đồng mẫu số, so sánh với 0 hoặc 1.
Bài 4 yêu cầu học sinh giải các bài toán thực tế liên quan đến số hữu tỉ. Bài tập này giúp học sinh áp dụng kiến thức về số hữu tỉ vào giải quyết các vấn đề trong cuộc sống, rèn luyện tư duy logic và khả năng giải quyết vấn đề.
Để giúp các em học sinh giải bài tập một cách dễ dàng và hiệu quả, chúng tôi sẽ cung cấp hướng dẫn giải chi tiết từng bài tập trong mục 1 trang 29, 30 SGK Toán 7 tập 1 - Kết nối tri thức.
Bài 1:
Bài 2:
Ví dụ: Tính (1/2) + (2/3). Để thực hiện phép cộng này, ta cần quy đồng mẫu số của hai phân số. Mẫu số chung nhỏ nhất của 2 và 3 là 6. Ta quy đồng hai phân số như sau:
(1/2) = (3/6)
(2/3) = (4/6)
Vậy, (1/2) + (2/3) = (3/6) + (4/6) = (7/6)
Bài 3:
Ví dụ: So sánh (-1/2) và (-1/3). Ta có thể quy đồng mẫu số của hai phân số. Mẫu số chung nhỏ nhất của 2 và 3 là 6. Ta quy đồng hai phân số như sau:
(-1/2) = (-3/6)
(-1/3) = (-2/6)
Vì -3 < -2 nên (-3/6) < (-2/6), hay (-1/2) < (-1/3).
Bài 4:
Bài toán: Một cửa hàng có 20 kg gạo. Ngày đầu bán được 1/4 số gạo, ngày thứ hai bán được 1/5 số gạo còn lại. Hỏi sau hai ngày, cửa hàng còn lại bao nhiêu kg gạo?
Giải:
Hy vọng rằng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin hơn trong việc giải các bài tập trong mục 1 trang 29, 30 SGK Toán 7 tập 1 - Kết nối tri thức. Chúc các em học tập tốt!